13.2.4 Crank-Nicolson Scheme
Crank-Nicolson Scheme. Dalam skema Crank-Nicolson, representasi yang lebih akurat dari istilah transien dihasilkan dengan mengekspresikan nilai-nilai fungsi T pada waktu dan
dalam hal nilai-nilai T dan turunannya pada waktu t

Maka, dengan mengurangkan dari
yang diberikan dalam Persamaan (13.35), diperoleh persamaan untuk turunan pertama sebagai:
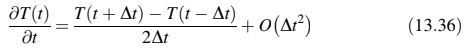
Perhatikan bahwa urutan akurasi turunannya sekarang adalah karena turunan orde kedua sepenuhnya dieliminasi.
Dengan mengganti turunan waktu yang diberikan oleh Persamaan (13.36) ke dalam Persamaan (13.3) diperoleh:

Kemudian, dengan memanggil hubungan aljabar dari operator spasial, dan menggunakan notasi yang disarankan, bentuk aljabar lengkap persamaan skalar transien diperoleh sebagai:

dengan koefisien yang diberikan oleh:

The stencil untuk Persamaan (13.38) ditunjukkan pada Figur 13.9. Jelas bahwa skema ini merupakan skema tipe eksplisit, karena evaluasi dari dapat dilakukan hanya dengan menggunakan nilai-nilai lama. Namun, dua tingkat lama sekarang diperlukan, dengan operator spasial dievaluasi pada salah satu dari tingkat tersebut.
Analisis stabilitas dari skema CN dapat dilakukan setelah sedikit memodifikasi persamaan asli. Menggunakan perkiraan berikut:

persamaan aljabar [Persamaan (13.38)] menjadi:

Oleh karena itu, kondisi stabilitas menjadi:
Untuk masalah adveksi transien satu dimensi yang ditampilkan dalam Figur 13.5, Persamaan (13.42) menghasilkan:

di mana diasumsikan bahwa istilah adveksi di-diskritisasi menggunakan skema hulu angin. Dengan menggunakan nomor CFL untuk konveksi yang didefinisikan di atas, Persamaan (13.43) diungkapkan sebagai:
Keterbatasan CFL yang lebih besar memuaskan, tetapi peningkatan akurasi justru lebih penting karena memungkinkan solusi yang akurat tanpa perlu mengandalkan langkah waktu yang sangat kecil, terutama karena turunan orde kedua sekarang dieliminasi dari kesalahan. Detail lebih lanjut mengenai analisis akurasi akan disajikan dalam bagian-bagian berikutnya.
