4.2. Nilai Tetap (Fixed Value) dan Gradien Tetap (Fixed Gradient)
Nilai tetap dan gradien tetap. Dalam persamaan untuk Ψ yang di-discretisasi untuk membentuk [A][Ψ]=[b] persamaan matriks , terdapat dua istilah yang mencakup properti yang diinterpolasi ke permukaan:
- Istilah adveksi dalam bentuk ∇.(uΨ) yang di-diskretisasi oleh Pers. (3.8) dalam bentuk ekstensif (lihat Bab. 3.5) seperti
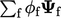
- Istilah Laplacian dalam bentuk ∇.(Γ∇Ψ) yang di-diskretisasi oleh Pers. (3.2) dalam bentuk ekstensif sebagai
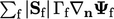 .
.
Istilah adveksi memerlukan nilai Ψ_f dan istilah Laplacian memerlukan gradien normal permukaan ∇_n Ψ_f di bagian permukaan. Ketika sebuah permukaan adalah bagian dari suatu tepi batas, setiap gradien ∇_n Ψ_f dan/atau nilai Ψ_f harus ditentukan melalui kondisi batas.
Nilai tetap, atau kondisi Dirichlet,1 adalah jenis pertama dari kondisi batas, di mana nilai batas Ψ_b ditentukan. Sebagai contoh, pada suatu tepi masuk, kita mungkin menentukan suhu T = 300 K dari fluida yang mengalir ke dalam domain.
Gradien tetap, atau kondisi Neumann,2 adalah jenis kedua, di mana gradien tegak lurus ke batas ∇_n Ψ_b ditentukan (di mana ∇_n ≡n∇). Dalam banyak kasus, gradien normal yang diterapkan adalah nol, yang merupakan kondisi umum yang diterapkan pada banyak bidang, termasuk T, pada suatu tepi keluar, yaitu di mana fluida mengalir keluar dari domain.
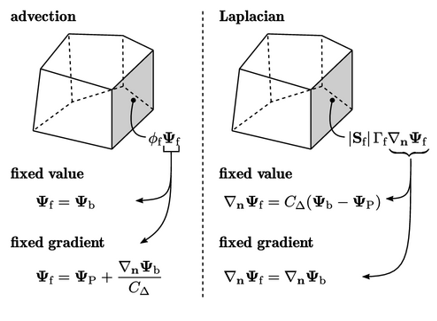
Ketika istilah adveksi di-diskretisasi, kondisi nilai tetap diterapkan dengan menggantikan nilai permukaan 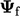 dengan nilai tepi
dengan nilai tepi 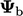 , yaitu mengatur
, yaitu mengatur 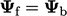 . Ketika suatu gradient tetap
. Ketika suatu gradient tetap 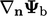 ditentukan, nilai wajah diungkapkan sebagai berikut, di mana
ditentukan, nilai wajah diungkapkan sebagai berikut, di mana 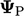 adalah nilai dalam sel yang berdekatan dengan setiap wajah:
adalah nilai dalam sel yang berdekatan dengan setiap wajah:
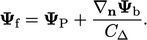 | (4.2) |
Ketika istilah Laplacian di-diskretisasi, kondisi batas gradient tetap diterapkan dengan menggantikan gradien normal permukaan 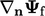 dengan gradien normal wajah patch
dengan gradien normal wajah patch 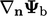 , yaitu mengatur
, yaitu mengatur 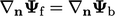 . Ketika nilai tetap
. Ketika nilai tetap 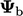 ditentukan, gradien normal permukaan diungkapkan oleh:
ditentukan, gradien normal permukaan diungkapkan oleh:
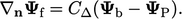 |
(4.3) |
