5.16 Prekondisi dan Asimetri

Prekondisi dan asimetri. Metode gradien konjugat (CG) memberikan dasar yang baik untuk solver matriks dalam CFD. Secara teoritis, metode ini memberikan solusi yang tepat dalam N langkah untuk masalah dengan N nilai. Namun, dalam praktiknya, terjadi akumulasi kesalahan pembulatan dari aritmatika presisi terbatas, sehingga solusi yang tepat tidak tercapai. Masalahnya juga terlalu besar sehingga tidak memungkinkan untuk menjalankan N langkah.

CG digunakan sebagai metode iteratif, bertujuan untuk mendapatkan residual solusi dalam toleransi yang dapat diterima. Tingkat konvergensi menjadi sangat penting, yang dapat ditunjukkan menjadi lebih lambat dengan peningkatan nilai kondisi matriks, k=λ_max/λ_min, di mana λ_max dan λ_min adalah eigenvalue terbesarnya.

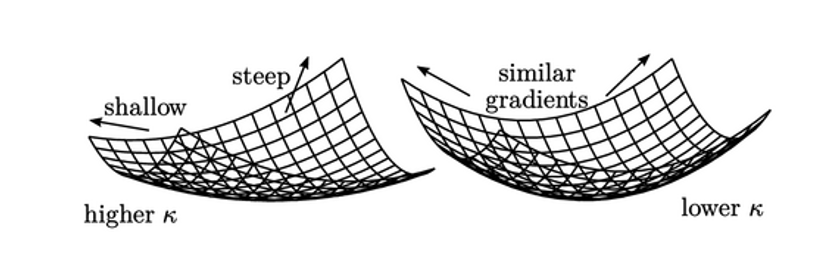
Pada contoh dengan dua nilai, eigenvalue berkorespondensi dengan gradien dari sumbu utama dari paraboloid yang dijelaskan oleh fungsi kuadratik. Nilai eigen yang lebih rendah berkorespondensi dengan gradien yang lebih dekat, yaitu bentuk “mangkuk” yang lebih bulat. Konvergensi terbaik berkorespondensi dengan 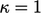ketika 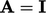( 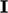adalah matriks identitas). Prekondisi menemukan matriks M, mirip dengan A, yang dapat diinverskan dan dikalikan dengan persamaan sebagai berikut:

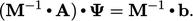$1 1 (M A) = M b: \relax \special {t4ht=$

(5.35)

Tujuan dari prekondisi adalah untuk meningkatkan konvergensi dengan memilih prekondisi 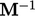sehingga 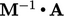lebih dekat dengan 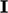daripada 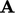. Metode efektif untuk menghitung prekondisi 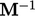adalah:

Diagonal-based incomplete Cholesky (DIC) untuk matriks simetris A;
Diagonal-based incomplete LU (DILU) untuk matriks asimetris A.

Metode biconjugate gradient stabilised (metode gradien bikonjugat yang distabilkan)

Metode CG yang telah diprekonduksi (PCG) meminimalkan bentuk kuadratik yang membutuhkan agar A bersifat simetris. Namun, setiap persamaan yang mengandung istilah adveksi menghasilkan matriks asimetris (lihat Bagian 5.1), di mana PCG tidak cocok.

Metode gradien bikonjugat yang telah diprekonduksi (PBiCG) dirancang untuk matriks asimetris. Metode ini memperluas perhitungan residu dan arah pencarian garis dalam metode CG dengan set kedua perhitungan yang terkait dengan matriks transpose 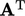. Biaya komputasinya sekitar 2× dari biaya PCG.

Perilaku konvergensi dari PBiCG agak tidak teratur, dengan variasi besar dalam penurunan residu antara iterasi berurutan. Terkadang metode ini mengalami kegagalan.

Metode gradien bikonjugat yang telah diprekonduksi dan distabilkan (PBiCGStab) merupakan modifikasi dari PBiCG. Metode ini menunjukkan konvergensi yang jauh lebih lancar dan keandalan yang lebih baik dibandingkan PBiCG, sehingga jauh lebih disukai untuk aplikasi CFD.

Metode berbasis CG yang direkomendasikan dirangkum sebagai berikut:

Untuk matriks simetris: PCG dengan prekondisi DIC.
Untuk matriks asimetris: PBiCGStab dengan prekondisi DILU.

Implementasi prekondisi dan metode berbasis CG dapat ditemukan di: Barrett R. et al. Templates for the solution of linear systems, tersedia di http://www.netlib.org.