5.18 Metode GAMG
Metode GAMG merupakan bentuk metode multi-grid yang efektif yang digunakan dalam CFD volume hingga. Metode ini mengombinasikan:
- aglomerasi geometris (“G”) untuk menentukan struktur mesh kasar;
- metode multi-grid aljabar (AMG), di mana matriks A dibentuk pada tingkat yang lebih kasar dari koefisien pada tingkat yang lebih halus, daripada menggunakan data geometris dari mesh kasar.
Aglomerasi
Aglomerasi berpasangan membentuk mesh yang lebih kasar dengan menggabungkan sepasang sel pada setiap tingkat pengkasaran. Dalam perjalanan melalui sel-sel, sel yang belum dipasangkan dipasangkan dengan tetangga (yang belum dipasangkan) yang memiliki luas permukaan bersama terbesar. Metode ini umumnya menjaga rasio aspek yang rendah (lihat Bagian 8.2) pada sel-sel yang dihasilkan dari aglomerasi tersebut.
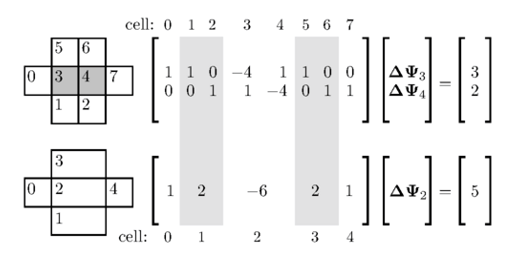
Contoh ini menunjukkan sebuah aglomerasi dari pasangan sel 1-2, 3-4, dan 5-6, yang membentuk sel 1, 2, dan 3 secara berurutan pada mesh kasar. Jika kita menyelesaikan persamaan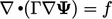 
pada mesh 2D dengan sel-sel persegi dengan 
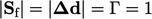, maka Persamaan (3.2) dan Persamaan (3.5) menghitung koefisien diagonal 
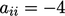dan koefisien off-diagonal non-nol 
.
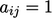Metode multi-grid aljabar (AMG) menciptakan koefisien pada mesh yang lebih kasar dengan menjumlahkan koefisien A dan sumber r dari mesh yang lebih halus. Contoh ini menghasilkan satu baris dari A yang merupakan |1 2 -6 2 1|.
Jika Laplacian untuk mesh kasar di-discretisasi secara langsung, maka koefisien dalam baris tersebut akan menjadi |2⁄3 2 -5 1⁄3 2 2⁄3| karena peningkatan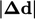 
. Diskrepansi antara koefisien yang diaglomerasi dan yang dihitung ini diulang dalam aglomerasi berikutnya.
Multi-grid dimulai dengan menyelesaikan/menghaluskan untuk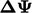 
(dengan 
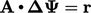) pada mesh terkasar. Nilai sel kasar dari 
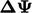kemudian disuntikkan ke sel yang sesuai pada mesh terhalus berikutnya.
Dengan istilah Laplacian, diskrepansi koefisien yang disebabkan oleh aglomerasi aljabar menyebabkan 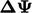menjadi terlalu rendah. Koreksi untuk 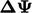dapat diterapkan dengan menskalakannya dengan faktor
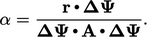 | (5.37) |
Penskalaan ini digunakan ketika persamaan yang sedang diselesaikan didominasi oleh istilah Laplacian, misalnya pada persamaan tekanan, ketika menjumlahkan koefisien antara sel-sel yang diaglomerasi tidak akurat. Penskalaan umumnya tidak digunakan untuk transportasi yang didominasi oleh adveksi, karena tidak ada kesalahan yang terkait dengan menjumlahkan koefisien dari turunan advektif.
Persamaan 5.37 diperoleh dengan meminimalkan kesalahan terhadap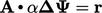 
dalam persamaan 
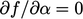. Minimisasi dilakukan dengan menetapkan eqn untuk bentuk kuadratik,
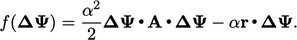 | (5.38) |