
5.7 Solusi Berulang
Solusi berulang. Bayangkan sebuah masalah dengan aliran yang stabil di mana T berubah di batas, misalnya di saluran masuk. Sistem tersebut dapat disimulasikan dengan memecahkan Persamaan (5.12) dengan medan u yang konstan dalam waktu.
Simulasi akan berkembang dengan urutan iteratif yang meningkatkan waktu t dengan penambahan ∆t, kemudian memecahkan persamaan, seperti yang ditunjukkan di bawah ini.
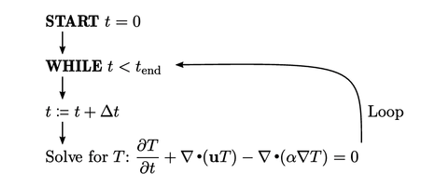
Setting Tolerance
Persamaan 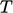 dipecahkan menggunakan metode iterasi seperti Gauss-Seidel. Parameter toleransi menentukuan hasil ketika metode berhenti beriterasi dalam solusi saat itu dijalankan.
dipecahkan menggunakan metode iterasi seperti Gauss-Seidel. Parameter toleransi menentukuan hasil ketika metode berhenti beriterasi dalam solusi saat itu dijalankan.
Untuk menangkap solusi transien untuk T secara akurat, persamaan tersebut perlu konvergen pada toleransi absolut yang sesuai 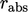 pada setiap langkah waktu. Pertanyaannya adalah:
pada setiap langkah waktu. Pertanyaannya adalah: 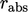 toleransi mana yang cocok untuk memberikan solusi yang akurat? — tanpa menetapkannya pada nilai yang sangat kecil, misalnya 10^(-15), yang akan sangat tidak efisien karena jumlah iterasi solver yang berlebihan.
toleransi mana yang cocok untuk memberikan solusi yang akurat? — tanpa menetapkannya pada nilai yang sangat kecil, misalnya 10^(-15), yang akan sangat tidak efisien karena jumlah iterasi solver yang berlebihan.
Akurasi solusi harus ditentukan oleh suatu ukuran, atau metrik, misalnya kenaikan suhu, penurunan tekanan, koefisien drag, dll., yang relevan dengan tujuan simulasi.
Metrik harus awalnya dihitung menggunakan nilai 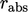 , misalnya 10^(-3). Kemudian dapat dihitung lagi pada nilai
, misalnya 10^(-3). Kemudian dapat dihitung lagi pada nilai 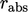 yang lebih rendah, biasanya berkurang satu orde magnitude, yaitu 10^(-4) .
yang lebih rendah, biasanya berkurang satu orde magnitude, yaitu 10^(-4) .
Kemudian metrik tersebut dibandingkan. Jika perbedaannya berada dalam tingkat akurasi yang diperlukan, maka 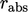 adalah yang optimal. Jika tidak,
adalah yang optimal. Jika tidak, 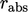 perlu dikurangi lebih lanjut dan proses diulang.
perlu dikurangi lebih lanjut dan proses diulang.
Perhitungan sisa pada interval
Perhitungan residu dari Persamaan (5.11) menimbulkan biaya komputasi yang signifikan karena melibatkan perkalian matriks. Biaya tersebut dapat dikurangi dengan menetapkan interval pada jumlah iterasi antara perhitungan residu.
Kekurangannya adalah pemeriksaan konvergensi hanya dapat terjadi saat residu dihitung. Jika residu dihitung pada interval setiap dua iterasi, sebuah solusi yang seharusnya konvergen pada jumlah iterasi ganjil akan menjadi lebih lama karena satu iterasi tambahan.

Residu tinggi saat memulai simulasi sehingga jumlah iterasi yang relatif tinggi, misalnya 10, mungkin diperlukan untuk konvergensi. Penghematan dalam menghitung residu pada interval kemudian dapat menutupi biaya tambahan dari iterasi tambahan yang tidak perlu, memberikan biaya bersih yang lebih rendah per langkah waktu. Namun, ketika residu semakin berkurang dan iterasi yang lebih sedikit diperlukan, upaya untuk mengurangi biaya dengan perhitungan residu secara periodik bisa menjadi tidak efektif atau kontraproduktif.
