
5.9 Sistem persamaan
Sistem persamaan. Sebagian besar perhitungan CFD melibatkan penyelesaian sistem persamaan yang merepresentasikan fisika dari masalah yang ada. Sebagai contoh, aliran laminar oleh konveksi alami dapat direpresentasikan oleh persamaan-persamaan yang diperkenalkan pada Bagian 2.20, yang direproduksi di bawah ini.
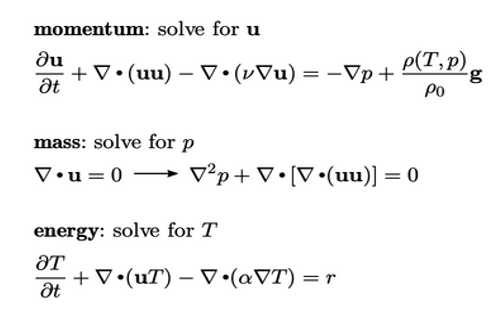
Sistem menyediakan 3 persamaan (1 vektor, 2 Skalar) yang bisa digunakan untuk memecahkan 3 variabel yang tidak diketahui 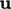 ,
, 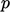 dan
dan 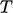
Seperti yang dibahas dalam Bagian 3.4, metode volume hingga menyelesaikan sebuah persamaan matriks individu untuk setiap variabel, misalnya 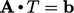 untuk
untuk 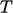 . Persamaan vektor untuk u diuraikan menjadi 3 persamaan matriks untuk komponen-komponen individu, yaitu
. Persamaan vektor untuk u diuraikan menjadi 3 persamaan matriks untuk komponen-komponen individu, yaitu 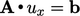 ,
, 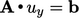 dan
dan 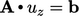 .
.
Setiap persamaan matriks individu untuk satu variabel solusi, misalnya 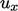 , mencakup istilah-istilah dari variabel lain, misalnya
, mencakup istilah-istilah dari variabel lain, misalnya 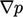 , ke dalam vektor sumber b. Kontribusi untuk b dihitung menggunakan nilai-nilai saat ini dari variabel yang bersangkutan. Sistem persamaan dipecahkan dengan substitusi berturut-turut dari variabel yang telah diselesaikan ke dalam vektor-vektor sumber persamaan-persamaan berikutnya.
, ke dalam vektor sumber b. Kontribusi untuk b dihitung menggunakan nilai-nilai saat ini dari variabel yang bersangkutan. Sistem persamaan dipecahkan dengan substitusi berturut-turut dari variabel yang telah diselesaikan ke dalam vektor-vektor sumber persamaan-persamaan berikutnya.
Solusi iteratif untuk sebuah persamaan tunggal, seperti yang dibahas dalam Bagian 5.7, dapat diperluas ke sistem persamaan. Waktu t ditingkatkan sebesar ∆t dan persamaan diselesaikan secara berurutan, sebelum kembali memulai langkah waktu berikutnya dengan peningkatan t.
Substitusi dalam persamaan momentum dan tekanan sangat penting, yang berakhir dalam koreksi u dan fluks advektif 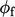 ,, seperti yang dibahas dalam Bagian 5.10.
,, seperti yang dibahas dalam Bagian 5.10.
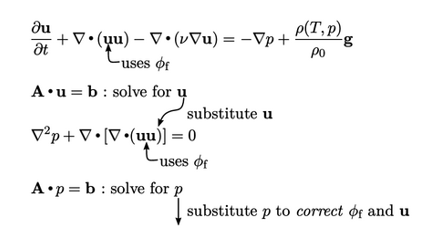
Pada awal langkah waktu apa pun, nilai saat ini 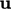 menjadi
menjadi 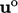 untuk diskritisasi dari istilah
untuk diskritisasi dari istilah 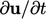 dalam persamaan momentum. Istilah adveksi
dalam persamaan momentum. Istilah adveksi 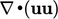 diskritisasi dengan Persamaan (3.8), memperlakukan satu u sebagai fluks
diskritisasi dengan Persamaan (3.8), memperlakukan satu u sebagai fluks 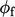 , dan yang lainnya sebagai jumlah yang diadveksi.
, dan yang lainnya sebagai jumlah yang diadveksi.
Persamaan diselesaikan untuk u. Solusi baru untuk u digantikan ke dalam persamaan p yang kemudian diselesaikan untuk p. Solusi baru untuk p kemudian digunakan untuk mengoreksi 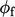 , untuk membantu menegakkan batasan konservasi massa
, untuk membantu menegakkan batasan konservasi massa 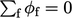 (
(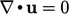 ).
).
Sebelum langkah solusi saat ini selesai, u juga dikoreksi untuk mengurangi kesalahan dalam diskritisasi 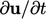 ketika nantinya menjadi
ketika nantinya menjadi 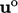 dalam langkah solusi berikutnya. Koreksi ini juga memberikan “tebakan awal” yang lebih baik u untuk solusi matriks dari persamaan momentum berikutnya, yang mengurangi waktu solusi.
dalam langkah solusi berikutnya. Koreksi ini juga memberikan “tebakan awal” yang lebih baik u untuk solusi matriks dari persamaan momentum berikutnya, yang mengurangi waktu solusi.
