Potensi Kecepatan
Untuk aliran irrotasional, gradien kecepatan terkait melalui Persamaan 6.59, 6.60, dan 6.61. Maka dalam kasus ini, komponen kecepatan dapat dinyatakan dalam bentuk fungsi skalar ∅(x, y, z, t) seperti yang ditunjukkan oleh rumus berikut:

Di mana ∅ disebut potensial kecepatan. Substitusi langsung dari ekspresi-ekspresi ini untuk komponen kecepatan ke dalam Persamaan 6.59, 6.60, dan 6.61 akan memverifikasi bahwa medan kecepatan yang didefinisikan oleh Persamaan 6.64 memang irrotasional. Dalam bentuk vektor, Persamaan 6.64 dapat ditulis sebagai:

sehingga untuk aliran irrotasional, kecepatan dapat dinyatakan sebagai gradien dari fungsi skalar ∅.
Potensial kecepatan adalah konsekuensi dari irrotasionalitas medan aliran, sedangkan fungsi aliran adalah konsekuensi dari kekekalan massa (lihat Bagian 6.2.3). Namun, perlu dicatat bahwa potensial kecepatan dapat didefinisikan untuk aliran tiga dimensi umum, sedangkan sebuah fungsi aliran tunggal dibatasi hanya untuk aliran dua dimensi.
Untuk fluida yang tidak dapat dikompres, kita tahu dari kekekalan massa bahwa
dan oleh karena itu untuk aliran tak dapat dikompres (dengan 𝑉 = ∇ ∅), maka berlaku
dimana ∇^2 ( )=∇∙∇ ( ) adalah operator Laplacian. Dalam koordinat kartesius

Persamaan diferensial ini muncul dalam banyak bidang rekayasa dan fisika dan disebut sebagai persamaan Laplace. Dengan demikian, medan aliran yang tidak berkepala, tak terkompres, dan tanpa rotasi diatur oleh persamaan Laplace. Jenis aliran ini umumnya disebut sebagai aliran potensial. Untuk menyelesaikan formulasi matematika dari suatu masalah yang diberikan, kondisi batas harus ditentukan. Ini biasanya merupakan kecepatan yang ditentukan pada batas-batas bidang aliran yang diminati. Ini mengikuti bahwa jika fungsi potensial dapat ditentukan, maka kecepatan di semua titik dalam bidang aliran dapat ditentukan dari Persamaan 6.64, dan tekanan di semua titik dapat ditentukan dari Persamaan Bernoulli. Meskipun konsep potensial kecepatan berlaku untuk aliran yang steady dan tidak steady, kami akan membatasi perhatian kami pada aliran yang steady.
Aliran potensial, yang diatur oleh Persamaan 6.64 dan 6.66, adalah aliran tanpa rotasi. Artinya, vortisitasnya nol di seluruhnya. Jika vortisitas hadir (misalnya, lapisan batas, sisa), maka aliran tidak dapat dijelaskan dengan persamaan Laplace. Gambar di samping mengilustrasikan aliran di mana vortisitas tidak nol di dua wilayah - wilayah terpisah di belakang tonjolan dan lapisan batas di sebelah permukaan padat. Ini dibahas secara detail dalam Bab 9.
Untuk beberapa masalah, akan nyaman menggunakan koordinat silindris, r, ∅, dan z. Dalam sistem koordinat ini, operator gradien adalah
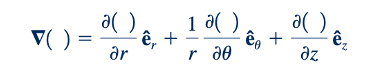
Sehingga
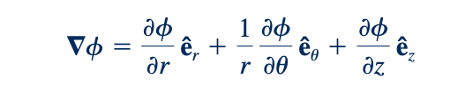
Dimana ∅=∅(𝑟, ∅,𝑧). Sejak

ini mengikuti untuk aliran tanpa rotasi (dengan V = ∇∅)

Juga, persamaan Laplace dalam koordinat silindris adalah




