Source and Sink
Untuk mempertahankan konservasi massa, laju aliran volume m harus merata secara radial sepanjang garis yang tegak lurus terhadap bidang x−y. Garis ini diperlihatkan dalam gambar 6.17.

Atau



Dikarenakan aliran adalah aliran murni radial, v𝜃= 0. Potensial kecepatan yang sesuai bisa diperoleh dengan mengintegrasikan persamaan tersebut.

Oleh karena itu

Jika m positif, aliran bergerak secara radial keluar, dan aliran dianggap sebagai aliran sumber. Jika m negatif, aliran menuju ke pusat, dan aliran dianggap sebagai aliran sumur. Laju aliran, m, adalah kekuatan dari sumber atau sumur.
Seperti yang ditunjukkan oleh gambar di samping, di titik asal dimana r sama dengan nol, kecepatan menjadi tak terhingga, yang tentunya secara fisik tidak mungkin. Oleh karena itu, sumber dan sumur sebenarnya tidak ada dalam medan aliran nyata, dan garis yang mewakili sumber atau sumur adalah singularitas matematis dalam medan aliran. Namun, beberapa aliran nyata dapat didekati di titik-titik jauh dari asal dengan menggunakan sumber atau sumur. Selain itu, potensial kecepatan yang mewakili aliran hipotetis ini dapat digabungkan dengan potensial kecepatan dasar lainnya untuk mendeskripsikan secara kasar beberapa medan aliran nyata. Ide ini lebih lanjut dibahas dalam Bagian 6.6.
Fungsi arus untuk sumber dapat diperoleh dengan mengintegrasikan hubungan-nya.


untuk menghasilkan
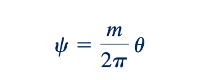
Dari Persamaan 6.83, terlihat bahwa garis-garis aliran (garis-garis konstan dari 𝜓) adalah garis-garis radial, sedangkan dari Persamaan 6.82 terlihat bahwa garis-garis ekuipotensial (garis-garis konstan dari ϕ) adalah lingkaran-linakran konsentris yang berpusat pada asal.


