numerical method

• Metode numerik digunakan dalam CFD untuk memecahkan persamaan tersebut karena solusi analitik dalam bentuk tertutup hanya ada untuk geometri yang sangat sederhana dan rezim aliran tertentu. Kumpulan Persamaan governing dan model digabungkan untuk mensimulasikan masalah aliran yang berbeda.
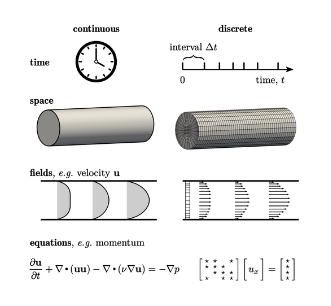
• Metode numerik menggambarkan entitas fisik yang kontinu dengan entitas diskrit yang setara, yaitu :

1.  Waktu dibagi menjadi interval dengan durasi Δt ,
2. Ruang menjadi sel-sel dari jaringan (mesh) – domain solusi,
3. Medan, misalnya u, menjadi nilai diskrit, misalnya satu per sel,
4. Persamaan diferensial parsial, misalnya untuk momentum, menjadi kumpulan persamaan linear.

•  Ada banyak metode diskritisasi untuk membuat kumpulan persamaan linear, tetapi literasi ini hanya mendiskusikan metode Volume Hingga (Finite Volume Method).
• Kumpulan persamaan tersebut dapat dipecahkan dengan menggunakan berbagai algoritma, di mana diskritisasi  metode Volume Hingga cenderung menggunakan metode iteratif.

Metode numerik dalam CFD memungkinkan insinyur dan ilmuwan untuk mengidentifikasi pola aliran yang kompleks, memprediksi performa sistem, dan merancang perangkat baru tanpa perlu melakukan percobaan fisik yang mahal. Dengan kemampuan ini, metode numerik dalam CFD telah menjadi alat yang tak ternilai dalam pengembangan teknologi dan inovasi di berbagai bidang, mulai dari rekayasa pesawat terbang dan mobil hingga desain bangunan dan peralatan medis.

Langkah pertama dalam menggunakan metode numerik dalam CFD adalah mendiskritisasi domain aliran menjadi grid atau jaringan. Selanjutnya, persamaan dasar dipecahkan secara iteratif di setiap titik grid untuk memperoleh solusi numerik. Teknik yang umum digunakan untuk memecahkan persamaan tersebut meliputi metode iteratif seperti metode iteratif Jacobi atau Gauss-Seidel, serta metode langsung seperti metode Gauss atau metode matriks.