Aliran Lapisan Batas Turbulen
Aliran lapisan batas turbulen. Struktur aliran lapisan batas turbulen sangat kompleks, acak, dan tidak teratur. Ini memiliki banyak karakteristik yang dijelaskan untuk aliran pipa turbulen di Bagian 8.3. Secara khusus, kecepatan di lokasi tertentu dalam aliran bersifat tidak tetap secara acak. Aliran ini dapat dianggap sebagai campuran yang kacau dari eddy yang terjalin satu sama lain dengan ukuran yang berbeda (diameter dan kecepatan sudut). Gambar di margin menunjukkan visualisasi fluoresensi yang diinduksi laser dari lapisan batas turbulen pada plat datar (dilihat dari samping). Berbagai kuantitas fluida yang terlibat (misalnya, massa, momentum, energi) diangkut ke arah hilir dalam arah aliran bebas seperti pada lapisan batas laminar. Untuk aliran turbulen, mereka juga diangkut melintasi lapisan batas (dalam arah tegak lurus terhadap plat) oleh transportasi acak partikel fluida berukuran terbatas yang terkait dengan eddy turbulen. Ada pencampuran yang signifikan terkait dengan eddy berukuran terbatas ini — jauh lebih banyak dibandingkan dengan pencampuran yang terkait dengan aliran laminar yang terbatas pada skala molekuler. Meskipun ada gerakan acak yang signifikan dari partikel fluida tegak lurus terhadap plat, ada sedikit transfer massa bersih melintasi lapisan batas — laju aliran terbesar jauh lebih besar sejajar dengan plat.
Namun, ada transfer bersih yang signifikan dari komponen x momentum tegak lurus terhadap plat karena gerakan acak partikel. Partikel fluida yang bergerak menuju plat (ke arah y negatif) memiliki beberapa momentum berlebihan (mereka berasal dari area kecepatan yang lebih tinggi) yang dihapus oleh plat. Sebaliknya, partikel yang menjauhi plat (ke arah y positif) mendapatkan momentum dari fluida (mereka berasal dari area kecepatan yang lebih rendah). Hasil bersihnya adalah bahwa plat bertindak sebagai penyerap momentum, terus-menerus mengekstrak momentum dari fluida. Untuk aliran laminar, transfer melintang aliran sifat ini terjadi semata-mata pada skala molekuler. Untuk aliran turbulen, ketidakpastian terkait dengan pencampuran partikel fluida. Akibatnya, gaya geser untuk aliran lapisan batas turbulen jauh lebih besar daripada aliran lapisan batas laminar (lihat Bagian 8.3).
Tidak ada solusi "tepat" untuk aliran lapisan batas turbulen. Seperti yang dibahas di Bagian 9.2.2, memungkinkan untuk menyelesaikan persamaan lapisan batas Prandtl untuk aliran laminar melintasi plat datar untuk mendapatkan solusi Blasius (yang "tepat" dalam kerangka asumsi yang terlibat dalam persamaan lapisan batas). Karena tidak ada ungkapan yang tepat untuk tegangan geser dalam aliran turbulen (lihat Bagian 8.3.2), solusi tidak tersedia untuk aliran turbulen. Namun, kemajuan besar telah dicapai dalam mendapatkan solusi numerik (komputer) untuk aliran turbulen dengan menggunakan hubungan tegangan geser perkiraan. Selain itu, kemajuan sedang dilakukan dalam area integrasi numerik langsung, lengkap dari persamaan dasar yang mengatur, yaitu persamaan Navier-Stokes.
Hasil perkiraan lapisan batas turbulen juga dapat diperoleh dengan menggunakan persamaan integral momentum, Persamaan 9.26, yang valid baik untuk aliran laminar maupun turbulen. Yang dibutuhkan untuk penggunaan persamaan ini adalah perkiraan yang masuk akal untuk profil kecepatan u = U g(Y), di mana Y = y/𝛿, dan u adalah kecepatan yang diaverase dalam waktu (notasi garis miring, u, dari Bagian 8.3.2 dihapus untuk kemudahan), dan hubungan fungsional yang menggambarkan tegangan geser dinding. Untuk aliran laminar, tegangan geser dinding digunakan sebagai 𝜏w = 𝜇(𝜕𝑢/𝜕𝑦)𝑦=0. Secara teori, teknik seperti ini seharusnya juga berfungsi untuk lapisan batas turbulen. Namun, seperti yang dibahas di Bagian 8.3, detail gradien kecepatan di dinding tidak dipahami dengan baik untuk aliran turbulen. Oleh karena itu, perlu menggunakan beberapa hubungan empiris untuk tegangan geser dinding. Ini diilustrasikan dalam Contoh 9.6.

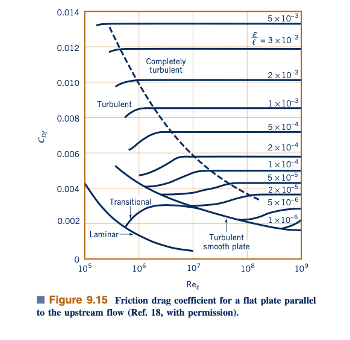
Secara umum, koefisien drag untuk plat datar dengan panjang ℓ adalah fungsi dari jumlah Reynolds, Reℓ, dan kekasaran relatif, 𝜀/ℓ. Hasil dari berbagai percobaan yang mencakup rentang luas parameter yang menarik ditunjukkan dalam Gambar 9.15. Untuk aliran lapisan batas laminar, koefisien drag adalah fungsi hanya dari jumlah Reynolds—kekasaran permukaan tidak penting. Ini mirip dengan aliran laminar dalam pipa. Namun, untuk aliran turbulen, kekasaran permukaan mempengaruhi tegangan geser dan, oleh karena itu, koefisien drag. Ini mirip dengan aliran turbulen dalam pipa di mana kekasaran permukaan dapat menonjol ke dalam atau melalui lapisan subviskosa di sebelah dinding dan mengubah aliran di lapisan tipis ini, tetapi sangat penting. Nilai kekasaran, 𝜀, untuk bahan-bahan yang berbeda dapat diperoleh dari Tabel 8.1.
Diagram koefisien drag dari Gambar 9.15 (aliran lapisan batas) memiliki banyak karakteristik yang umum dengan diagram Moody yang familiar (aliran pipa) dari Gambar 8.23, meskipun mekanisme yang mengatur aliran sangat berbeda. Aliran pipa horizontal yang sepenuhnya berkembang diatur oleh keseimbangan antara gaya tekanan dan gaya viskos. Inersia fluida tetap konstan sepanjang aliran. Aliran lapisan batas pada plat datar horizontal diatur oleh keseimbangan antara efek inersia dan gaya viskos. Tekanan tetap konstan sepanjang aliran. (Seperti yang dibahas di Bagian 9.2.6, untuk aliran lapisan batas pada permukaan lengkung, tekanan tidak konstan.)
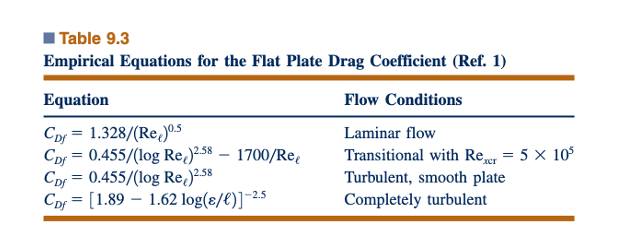
Seringkali nyaman memiliki persamaan untuk koefisien drag sebagai fungsi dari jumlah Reynolds dan kekasaran relatif daripada representasi grafis yang diberikan dalam Gambar 9.15. Meskipun tidak ada satu persamaan yang valid untuk seluruh rentang Reℓ - 𝜀/ℓ, persamaan yang disajikan dalam Tabel 9.3 berfungsi dengan baik untuk kondisi yang ditunjukkan.