Sirkulasi
Karena efek viskositas tidak terlalu penting dalam pembangkitan angkat, seharusnya mungkin untuk menghitung gaya angkat pada sebuah airfoil dengan mengintegrasikan distribusi tekanan yang diperoleh dari persamaan yang mengatur aliran inviskid melintasi airfoil. Artinya, teori aliran potensial yang dibahas dalam Bab 6 seharusnya memberikan metode untuk menentukan angkat. Meskipun detailnya di luar lingkup buku ini, berikut ini yang ditemukan dari perhitungan semacam itu (Ref. 42).
Perhitungan aliran inviskid melintasi sebuah airfoil dua dimensi memberikan medan aliran seperti yang ditunjukkan dalam Gambar 9.36. Medan aliran yang diprediksi melintasi sebuah airfoil tanpa angkat (yaitu, sebuah airfoil simetris pada sudut serang nol, Gambar 9.36a) tampaknya cukup akurat (kecuali untuk ketiadaan daerah lapisan batas tipis). Namun, seperti yang ditunjukkan dalam Gambar 9.36b, aliran yang dihitung melintasi airfoil yang sama pada sudut serang tak nol (tapi cukup kecil sehingga pemisahan lapisan batas tidak terjadi) tidaklah benar di dekat trailing edge. Selain itu, angkat yang dihitung untuk sudut serang tak nol adalah nol - bertentangan dengan fakta yang diketahui bahwa airfoil semacam itu menghasilkan angkat.
Secara realitas, aliran seharusnya berjalan lancar di atas permukaan atas seperti yang ditunjukkan dalam Gambar 9.36c, tanpa perilaku aneh yang ditunjukkan di dekat trailing edge dalam Gambar 9.36b. Seperti yang ditunjukkan dalam Gambar 9.36d, situasi aliran yang tidak realistis dapat diperbaiki dengan menambahkan aliran berputar searah jarum jam yang tepat di sekitar airfoil. Hasilnya adalah dua kali lipat: (1) Perilaku yang tidak realistis di dekat trailing edge dihilangkan (yaitu,
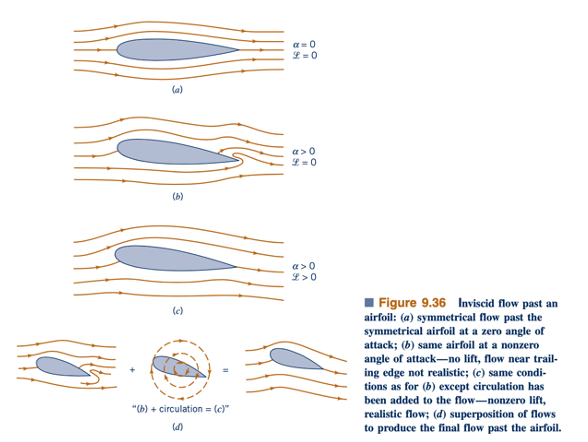
Pola aliran dari Gambar 9.36b diubah menjadi Gambar 9.36c, dan kecepatan rata-rata di permukaan atas airfoil meningkat sementara itu di permukaan bawah menurun. Dari konsep persamaan Bernoulli (yaitu, 𝜌/𝛾+𝑉2/2𝑔+𝑧 =konstan), tekanan rata-rata di permukaan atas berkurang sementara di permukaan bawah meningkat. Dampak keseluruhan adalah mengubah kondisi angkat nol asli menjadi kondisi airfoil yang menghasilkan angkat.
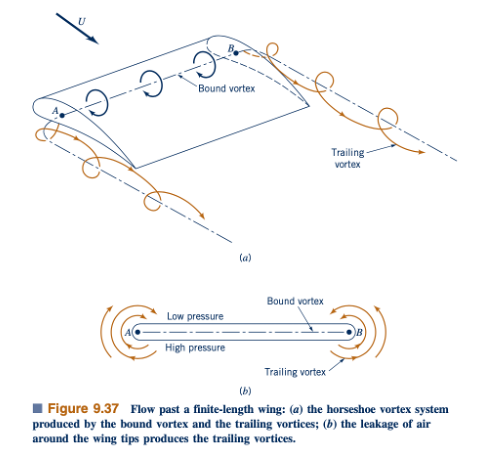
Penambahan pusaran searah jarum jam disebut penambahan sirkulasi. Jumlah pusaran yang dibutuhkan untuk membuat aliran keluar dari tepi belakang dengan mulus adalah fungsi dari ukuran dan bentuk airfoil dan dapat dihitung dari teori aliran potensial (inviscid) (lihat Bagian 6.6.3 dan Ref. 292). Meskipun penambahan sirkulasi untuk membuat medan aliran menjadi fisik secara realistis mungkin terlihat buatan, itu memiliki dasar matematis dan fisik yang kokoh. Sebagai contoh, pertimbangkan aliran melintasi airfoil berukuran terbatas, seperti yang ditunjukkan dalam Gambar 9.37. Untuk kondisi pembangkitan angkat, tekanan rata-rata di permukaan bawah lebih besar daripada di permukaan atas. Di dekat ujung sayap, perbedaan tekanan ini akan menyebabkan sebagian fluida berusaha bermigrasi dari permukaan bawah ke atas, seperti yang ditunjukkan dalam Gambar 9.37b. Pada saat yang sama, fluida ini dihanyutkan ke hilir, membentuk pusaran belakang dari setiap ujung sayap (lihat Gambar 4.32). Diperkirakan bahwa alasan beberapa burung bermigrasi dalam formasi V adalah untuk memanfaatkan udara naik yang dihasilkan oleh pusaran belakang dari burung sebelumnya. [Dihitung bahwa untuk pengeluaran energi yang diberikan, kawanan 25 burung yang terbang dalam formasi V bisa terbang 70% lebih jauh daripada jika setiap burung terbang secara terpisah (Ref. 152)].
Pusaran belakang dari ujung sayap kanan dan kiri terhubung oleh pusaran terikat sepanjang sayap. Inilah pusaran yang menghasilkan sirkulasi yang menghasilkan angkat. Sistem pusaran gabungan (pusaran terikat dan pusaran belakang) disebut sebagai pusaran kuda. Kekuatan dari pusaran belakang (yang sama dengan kekuatan pusaran terikat) sebanding dengan angkat yang dihasilkan. Pesawat besar (misalnya, Boeing 747) dapat menghasilkan pusaran belakang yang sangat kuat yang bertahan lama sebelum efek viscous dan mekanisme ketidakstabilan akhirnya membuatnya padam. Pusaran-pusaran tersebut cukup kuat untuk menjungkirbalikkan pesawat kecil jika mereka terbang terlalu dekat di belakang pesawat besar. Gambar di samping dengan jelas menunjukkan pusaran belakang yang dihasilkan selama studi pusaran bangun di mana pesawat terbang melalui kolom asap.
Seperti yang diindikasikan di atas, pembangkitan angkat secara langsung berkaitan dengan produksi aliran pusaran atau vortex di sekitar objek. Sebuah airfoil nonsimetris, yang didesain, menghasilkan jumlah pusaran dan angkat yang ditentukan sendiri. Sebuah objek simetris seperti silinder bulat atau bola, yang biasanya tidak memberikan angkat, dapat menghasilkan pusaran dan angkat jika berputar.
Seperti yang dibahas dalam Bagian 6.6.3, aliran inviscid melintasi silinder bulat memiliki pola aliran simetris seperti yang ditunjukkan dalam Gambar 9.38a. Secara simetri angkat dan drag adalah nol. Namun, jika silinder diputar sekitar sumbunya dalam fluida nyata diam 𝜇 ≠ 0, rotasi akan menyeret sebagian fluida sekitarnya, menghasilkan sirkulasi di sekitar silinder seperti yang terlihat pada Gambar 9.38b. Ketika sirkulasi ini digabungkan dengan aliran masuk ideal dan seragam, pola aliran seperti yang ditunjukkan dalam Gambar 9.38c diperoleh. Aliran tidak lagi simetris sekitar bidang horizontal melalui pusat silinder; tekanan rata-rata lebih besar di setengah bawah silinder daripada di setengah atas, dan angkat dihasilkan. Efek ini disebut sebagai efek Magnus, dari nama Heinrich Magnus (1802 - 1870), seorang kimiawan dan fisikawan Jerman yang pertama kali menyelidiki fenomena ini. Angkat yang sama dihasilkan pada bola yang berputar. Ini menjelaskan berbagai jenis lemparan dalam bisbol 1misalnya, bola curve, floater, sinker, dll.², kemampuan seorang pemain sepak bola untuk membelokkan bola, dan belokan atau slice dari bola golf.
Koefisien angkat dan drag tipikal untuk bola yang berputar halus ditunjukkan dalam Gambar 9.39. Meskipun koefisien drag relatif independen dari laju rotasi, koefisien angkatnya sangat kuat.
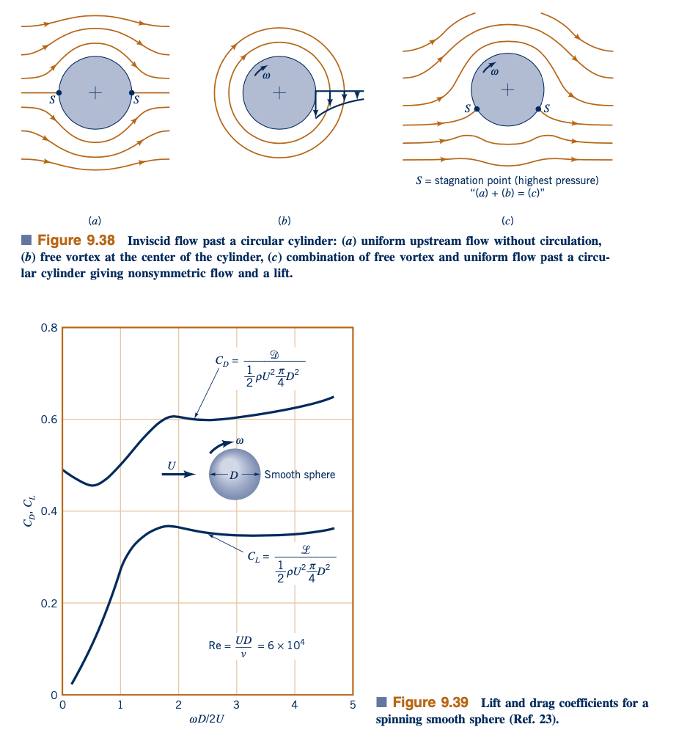
Kedua CL dan CD juga tergantung pada kekasaran permukaan, meskipun tidak ditunjukkan dalam gambar. Seperti yang dibahas di Bagian 9.3, dalam rentang nomor Reynolds tertentu, peningkatan kekasaran permukaan sebenarnya mengurangi koefisien drag. Demikian pula, peningkatan kekasaran permukaan dapat meningkatkan koefisien angkat karena kekasaran membantu menarik lebih banyak fluida di sekitar bola, meningkatkan sirkulasi untuk kecepatan sudut yang diberikan. Dengan demikian, bola golf yang berputar dan kasar dapat terbang lebih jauh daripada yang halus karena drag lebih kecil dan angkat lebih besar. Namun, jangan berharap bola yang sangat kasar akan lebih baik - telah dilakukan pengujian ekstensif untuk mendapatkan kekasaran permukaan yang optimal untuk bola golf.


