Energi Spesifik
Konsep energi spesifik atau kepala spesifik, E, didefinisikan sebagai:
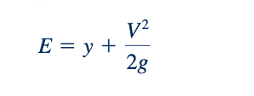
Konsep energi spesifik atau kepala spesifik, E, yang didefinisikan sebagai
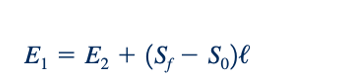
Jika kerugian kepala diabaikan, maka S=0 sehingga (Sf- So)ℓ = - S0ℓ = z2- z1 dan jumlah energi spesifik dan elevasi dasar saluran tetap konstan, yaitu merupakan pernyataan dari persamaan Bernoulli. Jika kita mempertimbangkan saluran sederhana yang bentuk penampang melintangnya adalah persegi panjang dengan lebar b, maka energi spesifik dapat dituliskan dalam bentuk aliran per unit lebar, q=Q/b=Vyb/b=Vy, sebagai
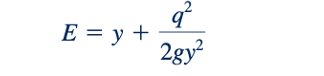
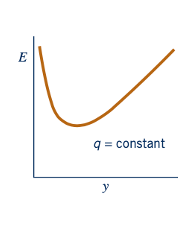
Ini diilustrasikan oleh gambar di pinggiran. Untuk saluran tertentu dengan lebar yang konstan, nilai q tetap konstan sepanjang saluran, meskipun kedalaman, y, dapat bervariasi. Untuk memperoleh wawasan tentang proses aliran yang terlibat, kita pertimbangkan diagram energi spesifik, sebuah grafik dari E= E(y), dengan q tetap, seperti yang ditunjukkan dalam Gambar 10.7. Hubungan antara kedalaman aliran, y, dan kepala kecepatan, V2/2g, seperti yang diberikan oleh Persamaan 10.8 ditunjukkan dalam gambar tersebut.
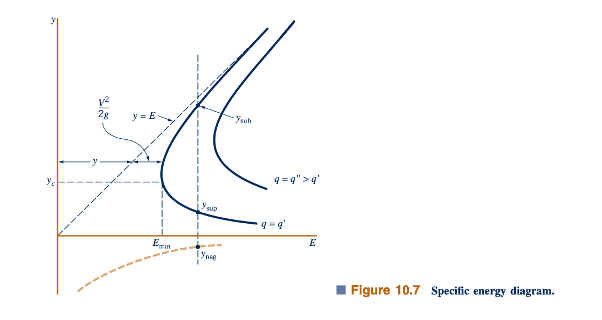
Untuk nilai q dan E tertentu, Persamaan 10.10 adalah persamaan kubik [y3 - Ey2 + (q2/2g) =0] dengan tiga solusi, y sup, y sub, dan y eg. Jika energi spesifik cukup besar (yaitu, E ≥ Eₘᵢₙ, di mana E min adalah fungsi dari q²), dua dari solusinya positif dan yang lain, y neg, negatif. Akar negatif, yang direpresentasikan oleh garis lengkung putus-putus dalam Gambar 10.7, tidak memiliki arti fisik dan dapat diabaikan. Dengan demikian, untuk laju aliran dan energi spesifik yang diberikan, ada dua kedalaman yang mungkin, kecuali jika garis vertikal dari sumbu E tidak berpotongan dengan kurva energi spesifik yang sesuai dengan nilai q yang diberikan (yaitu, E ≤ Eₘᵢₙ). Kedua kedalaman ini disebut kedalaman alternatif.
Untuk nilai E yang besar, cabang atas dan bawah dari diagram energi spesifik (y sub dan y sup) mendekati y =E dan y = 0, secara berturut-turut. Batas ini sesuai dengan saluran yang sangat dalam dengan aliran yang sangat lambat (E = y + V²/2g saat y mendekati ∞ dengan q = Vy tetap), atau aliran yang sangat cepat di saluran dangkal (E = y + V²/2g saat y mendekati 0).
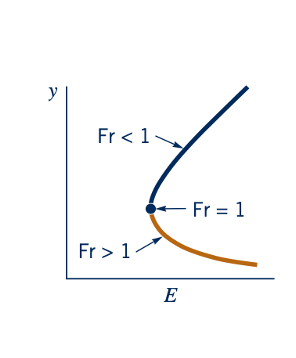
Seperti yang ditunjukkan dalam Gambar 10.7, y sup ≤ y sub. Oleh karena itu, karena q = Vy konstan sepanjang kurva, dapat disimpulkan bahwa V sup > V sub, di mana tanda "sub" dan "sup" pada kecepatan sesuai dengan kedalaman yang ditunjukkan. Diagram energi spesifik terdiri dari dua bagian yang dipisahkan oleh "hidung" Emin dari kurva. Kami akan menunjukkan bahwa kondisi aliran di lokasi ini sesuai dengan kondisi kritis (Fr = 1), yang pada bagian atas kurva sesuai dengan kondisi subkritis (maka, tanda "sub"), dan yang pada bagian bawah kurva sesuai dengan kondisi superkritis (maka, tanda "sup").
Untuk menentukan nilai Emin, kita menggunakan Persamaan 10.10 dan mengatur dE/dy = 0 untuk mendapatkan
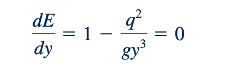
Atau
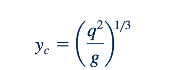
yang mana "c" menunjukkan kondisi pada Emin. Dengan mensubstitusikan ini kembali ke Persamaan 10.10, kita memperoleh:
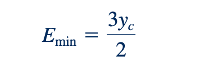
Dengan menggabungkan Persamaan 10.11 dan Vc = q/ yc, kita dapatkan :
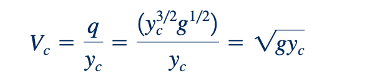
atau Frc = Vc/(gyc)^1/2 =0 . Dengan demikian, kondisi kritis (Fr =1/2) terjadi di lokasi E min. Karena lapisan lebih dalam dan kecepatan lebih kecil untuk bagian atas diagram energi spesifik (dibandingkan dengan kondisi di Emin), aliran tersebut adalah subkritis (Fr < 1/2). Sebaliknya, aliran untuk bagian bawah diagram adalah superkritis. Ini ditunjukkan oleh gambar di pinggir halaman. Jadi, untuk laju aliran tertentu, q, jika E > Emin ada dua kedalaman aliran yang mungkin, satu subkritis dan yang lainnya superkritis.
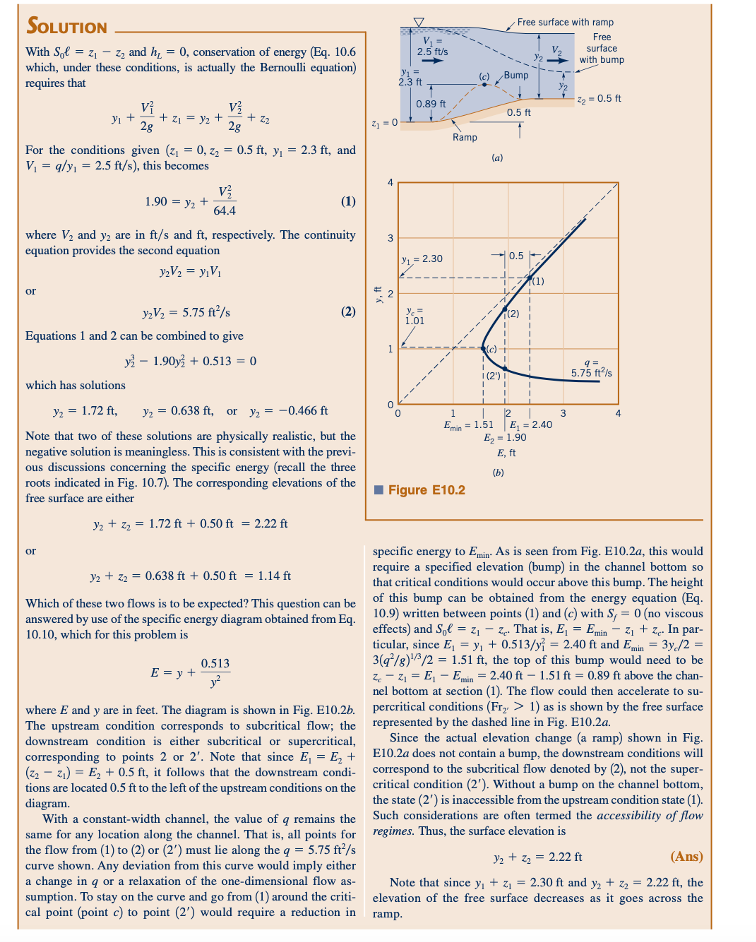
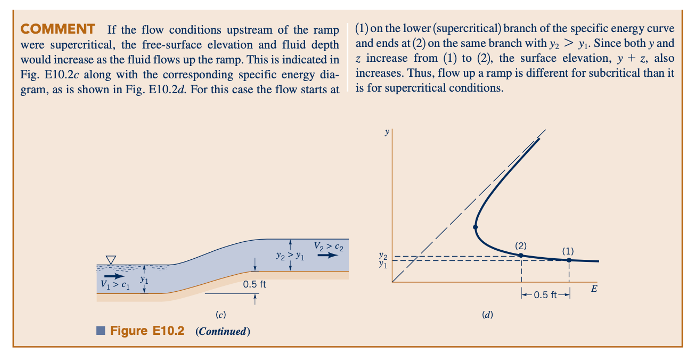
Seringkali memungkinkan untuk menentukan berbagai karakteristik aliran dengan mempertimbangkan diagram energi spesifik. Contoh 10.2 mengilustrasikan hal ini untuk situasi di mana elevasi dasar saluran tidak konstan.