Contoh Kedalaman Seragam
Contoh kedalaman seragam. Berbagai hasil menarik dan berguna dapat diperoleh dari persamaan Manning. Contoh-contoh berikut mengilustrasikan beberapa pertimbangan yang tipikal.
Parameter utama yang terlibat dalam aliran saluran terbuka dengan kedalaman seragam adalah ukuran dan bentuk penampang lintang saluran (A, Rh), kemiringan dasar saluran (S0), sifat material yang melapisi dasar dan dinding saluran (n), serta kecepatan rata-rata atau laju aliran (V atau Q). Meskipun persamaan Manning adalah persamaan yang cukup sederhana, kemudahan penggunaannya bergantung pada sebagian pada variabel mana yang diberikan dan mana yang akan ditentukan.
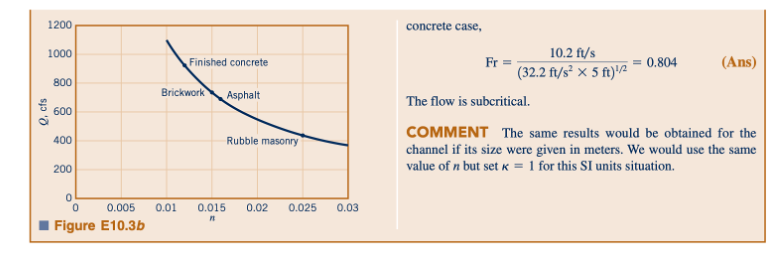
Penentuan laju aliran dari saluran tertentu dengan aliran pada kedalaman tertentu (sering disebut sebagai laju aliran normal untuk kedalaman normal, kadang-kadang ditandai sebagai yn) diperoleh dari perhitungan langsung seperti yang ditunjukkan dalam Contoh 10.3.

Dalam beberapa kasus, metode coba-coba atau iterasi harus digunakan untuk memecahkan variabel dependen. Hal ini sering terjadi ketika laju aliran, kemiringan saluran, dan material saluran telah diberikan, dan kedalaman aliran harus ditentukan seperti yang diilustrasikan dalam contoh-contoh berikut.
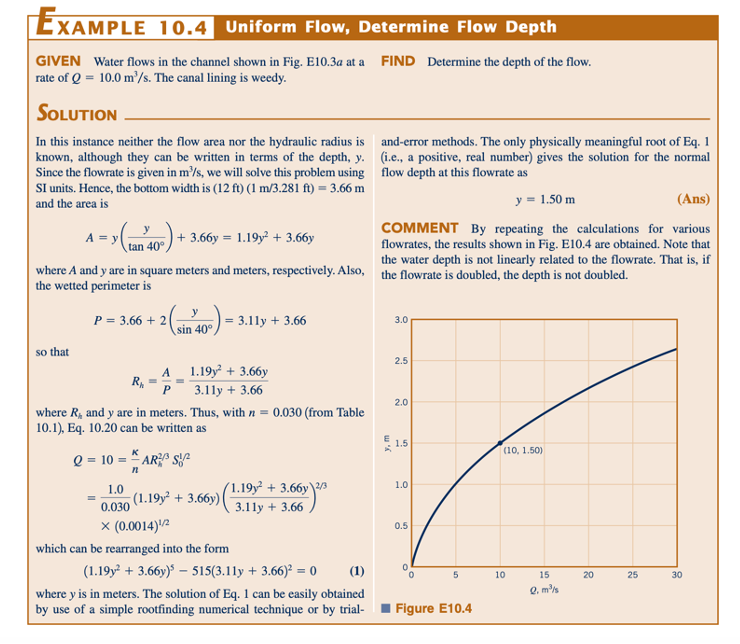
Pada Contoh 10.4, kita menemukan kedalaman aliran untuk laju aliran yang diberikan. Karena persamaan untuk kedalaman ini adalah persamaan nonlinier, mungkin ada lebih dari satu solusi untuk masalah tersebut. Untuk saluran tertentu, mungkin ada dua atau lebih kedalaman yang membawa laju aliran yang sama. Meskipun ini tidak biasanya terjadi, hal ini bisa terjadi, seperti yang diilustrasikan dalam Contoh 10.5.

Pada banyak saluran buatan dan sebagian besar saluran alami, kekasaran permukaan (dan, oleh karena itu, koefisien Manning) bervariasi sepanjang garis basah saluran. Sebuah parit drainase, misalnya, mungkin memiliki permukaan dasar yang berbatu dengan dinding samping beton untuk mencegah erosi. Dengan demikian, nilai efektif n akan berbeda untuk kedalaman dangkal dibandingkan untuk kedalaman aliran yang dalam. Demikian pula, saluran sungai mungkin memiliki satu nilai n yang sesuai untuk saluran normalnya dan nilai n yang sangat berbeda ketika banjir terjadi, di mana sebagian aliran melintasi lapangan atau melalui hutan banjir. Saluran yang tertutup es biasanya memiliki nilai n yang berbeda untuk es daripada untuk bagian lain dari garis basah (52). Secara ketat, saluran yang tertutup es tersebut bukanlah saluran "terbuka", meskipun analisis alirannya sering kali didasarkan pada persamaan aliran saluran terbuka. Hal ini dapat diterima, karena penutup es seringkali cukup tipis sehingga mewakili batas yang tetap dalam hal resistansi gaya gesek, tetapi tidak dapat mendukung perbedaan tekanan yang signifikan seperti dalam situasi aliran pipa.
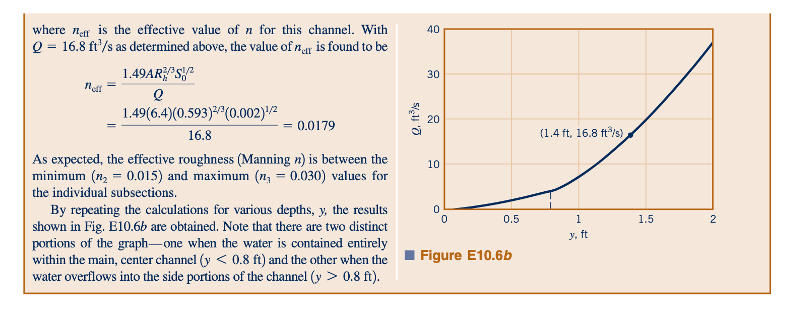
Berbagai metode telah digunakan untuk menentukan nilai kasar yang efektif dari saluran yang mengandung subbagian dengan nilai n yang berbeda. Metode mana yang memberikan hasil yang paling akurat dan mudah digunakan belum pasti, karena hasilnya hampir sama untuk setiap metode. (52) Suatu perkiraan yang masuk akal adalah dengan membagi penampang saluran menjadi N subbagian, masing-masing dengan garis basahnya sendiri, Pi, luasnya, Ai, dan koefisien Manning, ni. Nilai-nilai Pi tidak termasuk batas-batas imajiner antara subbagian yang berbeda. Laju aliran total diasumsikan sebagai jumlah dari laju aliran melalui setiap bagian. Teknik ini diilustrasikan oleh Contoh 10.7.

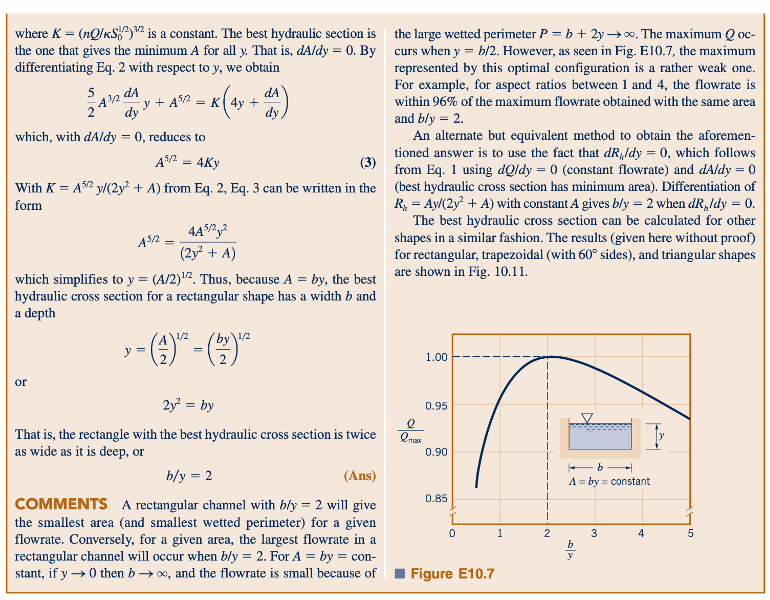
Salah satu jenis masalah yang sering dihadapi dalam aliran saluran terbuka adalah menentukan penampang lintang hidrolik terbaik, yang didefinisikan sebagai penampang dengan luas minimum untuk laju aliran, Q, kemiringan, S0, dan koefisien kekasaran, n, yang diberikan. Dengan menggunakan Rh = A/P, kita dapat menulis Persamaan 10.20 sebagai
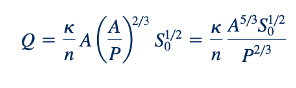
Ini dapat diubah menjadi:
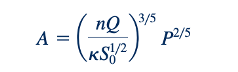
di mana jumlah dalam tanda kurung adalah konstan. Dengan demikian, saluran dengan A minimum adalah saluran dengan P minimum, sehingga baik jumlah galian yang dibutuhkan maupun jumlah material yang diperlukan untuk melapisi permukaan diminimalkan oleh penampang lintang hidrolik terbaik.
Penampang lintang hidrolik terbaik yang mungkin adalah saluran setengah lingkaran. Tidak ada bentuk lain yang memiliki garis basah sekecil ini untuk luas tertentu. Seringkali diinginkan untuk menentukan bentuk terbaik untuk sebuah kelas penampang. Hasil untuk bentuk-bentuk persegi, trapesium (dengan sisi-sisi 60°), dan segitiga ditunjukkan dalam Gambar 10.11. Sebagai contoh, penampang lintang hidrolik terbaik untuk sebuah persegi adalah yang kedalamannya setengah dari lebarnya; untuk sebuah segitiga adalah segitiga 90°.