5.4 Sisa

Sisa. Pada Bagian 5.3, kita menetapkan suatu kriteria konvergensi untuk metode Gauss-Seidel. Sekarang kita memerlukan cara untuk memperkirakan tingkat konvergensi untuk menentukan kapan harus menghentikan iterasi.

Analisis konvergensi berpusat pada kesalahan solusi ϵ_i yang diperkenalkan di Bagian 5.2. Pada praktiknya, ϵ_i tidak dapat ditentukan karena solusi yang tepat tidak diketahui. Sebagai gantinya, residu memberikan ukuran akurasi solusi. Vektor residu r mewakili perubahan pada solusi persamaan, diperlukan untuk membuat ψ menjadi tepat, sesuai dengan,

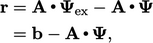r = A ex A = b A ; \relax \special {t4ht=

(5.10)

dimana .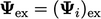

Untuk sisa bab ini, notasi matriks 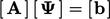diganti dengan 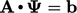, yang setara dengan notasi vektor dengan N x N tensor A. Vektor r (dengan ukuran N) menyediakan satu nilai per baris matriks, dengan nilai positif dan negatif. Pengukuran residu yang diberikan oleh satu nilai, didefinisikan sebagai,

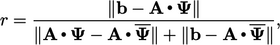------kb----A------k--------- r = kA A --k+ kb A -k ; \relax \special {t4ht=

(5.11)

di mana ‖. . . . .‖ adalah norma matriks, dihitung sebagai jumlah dari magnitudo setiap komponen, misalnya 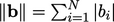; nilai rata-rata dari 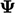di seluruh sel dinotasikan dengan .

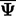Residu r memberikan ukuran kesalahan dalam solusi dari 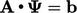, bukan kesalahan absolut 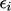. Ini dibagi oleh norma dan 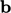untuk mengurangi ketergantungannya pada skala geometri dan variabel solusi. Dengan mengurangi ketergantungan terhadap skala, r dapat digunakan untuk membandingkan tingkat kesalahan secara adil antara simulasi pada skala yang berbeda.

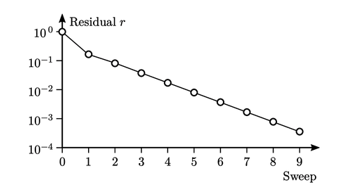
Gambar di atas menunjukkan r yang dihitung dari Persamaan (5.11) mengikuti iterasi berulang metode Gauss-Seidel (dimulai dari nilai awal r=1). Grafik menggunakan skala vertikal logaritmik karena nilai-nilai dari r meluas lebih dari 4 orde magnitude.

Toleransi

Perangkat lunak CFD umumnya menyediakan kontrol berikut untuk menghentikan solver iteratif:

toleransi absolut ;
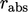toleransi relatif .

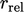Iterasi akan berhenti jika salah satu kondisi toleransi terpenuhi: 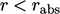; atau 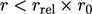di mana 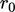adalah residu awal dalam langkah solusi tertentu. Kriteria 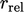sering dinonaktifkan dengan menetapkan 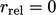, terutama untuk simulasi transien ketika akurasi yang memadai diperlukan pada setiap langkah solusi.