5.12 Solusi keadaan tunak
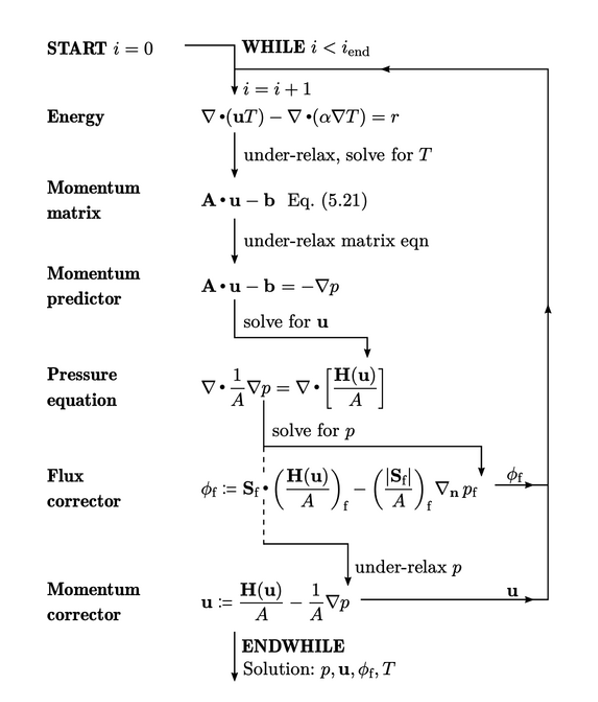
Solusi keadaan tunak. Algoritma SIMPLE (Semi-Implicit Method for Pressure-Linked Equations)3 menggabungkan persamaan dalam Bagian 5.10 dengan menggunakan algoritma yang menghubungkan solusi untuk p dan u. Algoritma ini disajikan di sini dengan interpretasi modern.
Algoritma SIMPLE umumnya digunakan untuk menghasilkan solusi aliran tunak dalam CFD. Solusi ini secara langsung dapat diterapkan untuk aliran yang mencapai keadaan tunak, yaitu ketika variabel aliran berhenti berubah dalam waktu. Mereka juga dapat memberikan solusi perkiraan untuk aliran yang moderat tidak stabil, biasanya dengan biaya yang lebih rendah dibandingkan solusi transien yang lebih tepat.
Sebuah contoh dari algoritma tersebut ditunjukkan untuk sistem persamaan yang disajikan di Bagian 5.9. Istilah turunan waktu (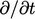 ) dihilangkan karena asumsi keadaan tunak.
) dihilangkan karena asumsi keadaan tunak.
Algoritma melibatkan urutan iteratif dengan langkah-langkah, i=1,2,. . .. ,i_end. Dimulai dengan membangun persamaan matriks untuk energi yang direlaksasi secara under oleh faktor 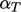 . Persamaan ini dipecahkan untuk T, yang digunakan untuk memperbarui
. Persamaan ini dipecahkan untuk T, yang digunakan untuk memperbarui 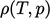 sesuai dengan persamaan keadaan. Kemudian, persamaan matriks dibangun menggunakan semua istilah dari persamaan momentum kecuali
sesuai dengan persamaan keadaan. Kemudian, persamaan matriks dibangun menggunakan semua istilah dari persamaan momentum kecuali 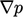 , yaitu
, yaitu
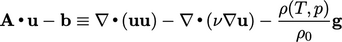 | (5.21) |
Persamaan matriks di-relaksasi di bawah faktor 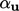 sebelum disejajarkan dengan
sebelum disejajarkan dengan 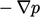 dan dipecahkan untuk u (prediktor momentum).
dan dipecahkan untuk u (prediktor momentum).
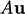 dan
dan 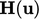 kemudian dievaluasi dari
kemudian dievaluasi dari 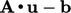 (matriks momentum), seperti yang dijelaskan pada halaman 351. Mereka digunakan untuk membentuk persamaan tekanan, yang dipecahkan untuk p.
(matriks momentum), seperti yang dijelaskan pada halaman 351. Mereka digunakan untuk membentuk persamaan tekanan, yang dipecahkan untuk p.
Tekanan baru p digunakan untuk memperbaiki aliran 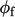 sehingga mematuhi konservasi massa dengan lebih baik (korektor aliran). Kemudian, persamaan tersebut di-relaksasi di bawah faktor
sehingga mematuhi konservasi massa dengan lebih baik (korektor aliran). Kemudian, persamaan tersebut di-relaksasi di bawah faktor 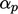 sebelum memperbaiki u sebelum langkah solusi berikutnya dimulai (korektor momentum).
sebelum memperbaiki u sebelum langkah solusi berikutnya dimulai (korektor momentum).