5.17 Metode multi-grid

Metode multi-grid. Metode yang telah dijelaskan untuk menyelesaikan persamaan matriks adalah Gauss-Seidel dan CG. Kedua metode tersebut bersifat iteratif dan memerlukan sedikit iterasi untuk menghitung perubahan di lapangan, ketika perubahan di titik manapun hanya dipengaruhi oleh titik-titik di sekitarnya.

Hal ini membuat mereka efisien untuk menyelesaikan persamaan yang jangkauan pengaruhnya terbatas, misalnya oleh kecepatan aliran melalui persamaan adveksi 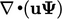dalam suatu persamaan transportasi.

Persamaan tekanan tidak mengandung perubahan laju lokal atau 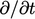istilah adveksi (diasumsikan ρ = constant). Gangguan di titik manapun memengaruhi solusi di seluruh domain secara instan, seperti yang dibahas di Bagian 4.3.

Untuk mentransfer perubahan di seluruh domain, metode Gauss-Seidel mungkin memerlukan sebanyak banyaknya pemindaian seperti jumlah sel di seluruh domain, yang akan menjadi tidak praktis. Oleh karena itu, diperlukan suatu metode yang mentransfer perubahan di seluruh domain dengan lebih efisien.

Metode multi-grid menggunakan mesh kasar untuk mengatasi masalah lambatnya transfer perubahan di seluruh domain, mengurangi kesalahan pada “frekuensi rendah”. Metode ini mentransfer solusi tersebut melalui sejumlah mesh yang lebih halus untuk menjadi akurat pada frekuensi yang lebih tinggi.

Metode multi-grid bekerja dengan pertama-tama menghitung matriks 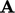dan vektor residu r pada mesh asli (terhalus). Mesh yang lebih kasar kemudian dibentuk secara berturut-turut sampai mesh mencapai tingkat terkasar, yang berisi sekitar 10 sel saja.

Matriks A dan r terbentuk pada setiap tingkat pengkasaran. Metode yang berbeda ada untuk menghitung A dan r, termasuk aglomerasi sederhana yang dibahas di Bagian 5.18.

Metode multi-grid bekerja dengan pertama-tama menghitung matriks A dan vektor residu r pada mesh asli (terhalus). Mesh yang lebih kasar kemudian dibentuk secara berturut-turut sampai mesh mencapai tingkat terkasar, yang berisi sekitar 10 sel saja.

Matriks A dan r terbentuk pada setiap tingkat pengkasaran. Metode yang berbeda ada untuk menghitung A dan r, termasuk aglomerasi sederhana yang dibahas di Bagian 5.18.

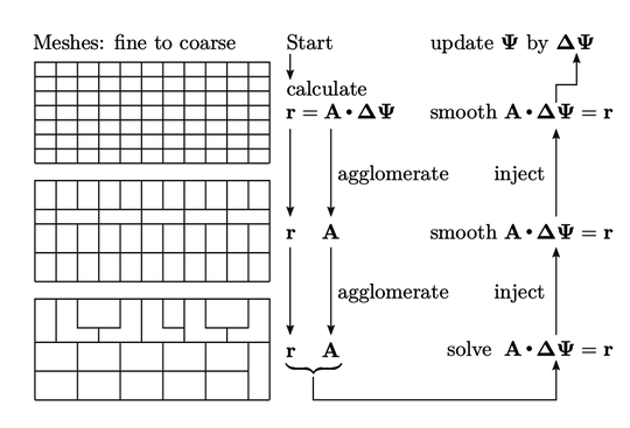
Persamaan dibentuk dalam hal koreksi 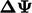, yang diperlukan untuk membuat 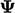menjadi tepat, terkait dengan residu r oleh ,

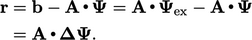$r = b A = A ex A = A : \relax \special {t4ht=$

(5.36)

Pada tingkat terkasar, 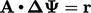dipecahkan secara tepat untuk 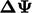, yang dapat dilakukan dengan efisien menggunakan solver langsung karena matriksnya kecil.

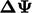kemudian disuntikkan ke tingkat yang lebih halus, memberikan nilai awal 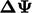untuk beberapa pemindaian metode Gauss-Seidel pada tingkat tersebut. Pelicinan dan penyuntikan diulang hingga ke tingkat terhalus, ketika 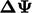final diterapkan ke 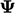untuk menghasilkan solusi.

Umumnya lebih efisien untuk melakukan lebih banyak pemindaian metode Gauss-Seidel pada tingkat yang lebih kasar, ketika biayanya rendah karena ukuran matriks yang lebih kecil. Misalnya, 4 pemindaian dapat diterapkan pada tingkat yang lebih kasar, sementara 2 pemindaian diterapkan pada tingkat terhalus.