
5.19 Solusi Transien
Solusi transien. Sebuah interpretasi modern dari algoritma SIMPLE telah dijelaskan dalam Bagian 5.12 untuk menggabungkan solusi steady untuk p dan u. Solusi transient yang setara mengikuti urutan iteratif di mana persamaan untuk p dan u dipecahkan selama interval waktu berturut-turut 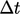 , antara waktu mulai
, antara waktu mulai 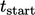 dan waktu selesai
dan waktu selesai 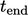 .
.
Dalam simulasi transient, 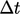 perlu relatif kecil untuk mempertahankan akurasi yang memadai saat solusi berkembang seiring waktu t. Persamaan-persamaan tersebut umumnya tidak memerlukan under-relaxation untuk konvergensi karena peningkatan
perlu relatif kecil untuk mempertahankan akurasi yang memadai saat solusi berkembang seiring waktu t. Persamaan-persamaan tersebut umumnya tidak memerlukan under-relaxation untuk konvergensi karena peningkatan 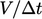 terhadap koefisien diagonal matriks dari diskritisasi turunan waktu
terhadap koefisien diagonal matriks dari diskritisasi turunan waktu 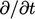 .
.
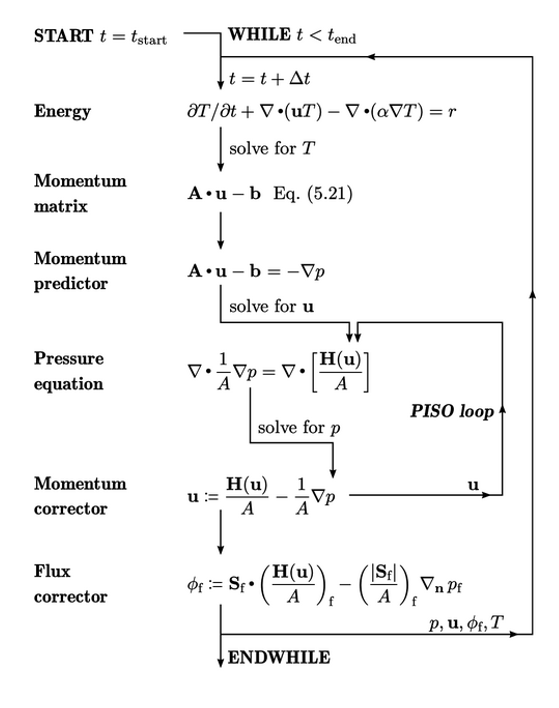
Sebuah simulasi transient dapat mengikuti urutan yang sama seperti algoritma SIMPLE pada halaman 359, namun melakukan iterasi atas urutan tersebut dalam setiap langkah waktu adalah biaya yang mahal. Sebuah algoritma yang lebih efisien menyelesaikan urutan tersebut hanya sekali per langkah waktu tetapi menambahkan lingkaran iteratif yang menggantikan u dari korektor momentum ke dalam istilah H(u) dari persamaan tekanan.
Persamaan tekanan kemudian dipecahkan untuk kedua kalinya, diikuti oleh korektor momentum kedua, dalam gaya algoritma PISO. Penambahan “loop PISO” ini meningkatkan akurasi dari p, u, dan 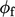 dalam setiap langkah waktu. u yang diperbaiki menjadi
dalam setiap langkah waktu. u yang diperbaiki menjadi 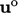 dalam iterasi waktu berikutnya, yang secara kritis meningkatkan akurasi dari turunan waktu
dalam iterasi waktu berikutnya, yang secara kritis meningkatkan akurasi dari turunan waktu 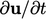 dalam persamaan momentum.
dalam persamaan momentum.
- Tanpa iterasi atas seluruh sistem persamaan, istilah adveksi diskritisasi menggunakan
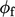 dari langkah waktu sebelumnya. “Penundaan” dari
dari langkah waktu sebelumnya. “Penundaan” dari 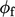 ini tidak secara signifikan mengompromikan akurasi, jika
ini tidak secara signifikan mengompromikan akurasi, jika 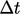 cukup kecil, misalnya yang sesuai dengan
cukup kecil, misalnya yang sesuai dengan 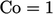 .
. - Sebuah iterasi tambahan dari loop PISO dapat diperkenalkan untuk menyelesaikan persamaan tekanan ketiga dan korektor momentum ketiga, khususnya sebagai bagian dari pembaruan terhadap non-ortogonalitas yang dijelaskan dalam Bagian 5.20. Meningkatkan iterasi lebih lanjut secara umum tidak bermanfaat.
