Forces at Surface

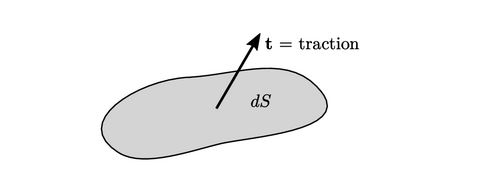
Hukum yang akan dibahas selanjutnya adalah hukum kekekalan momentum, yaitu hukum kedua newton tentang gerak (f = m a) pada fluida. Hukum ini melibatkan gaya – gaya di dalam fluida, sehingga memerlukan deskripsi tentang gaya pada suatu permukaan (S) yang membatasi suatu volume (V).

Gaya ( 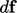$\text{[math]}$ ) berada dalam arah vektor tarikan dengan magnitudo (tarikan x luas permukaan) – dibandingkan dengan persamaan (2.3)

df = tdS \relax \special {t4ht=

(2.16)

Tarikan pada suatu permukaan yang membatasi suatu volume fluida (atau kontinum apapun, misalnya padatan) bergantung pada orientasi permukaan tersebut. Oleh karena itu, kita tidak dapat mendefinisikan gaya dalam suatu fluida sebagai vektor tarikan pada titik-titik dalam fluida.

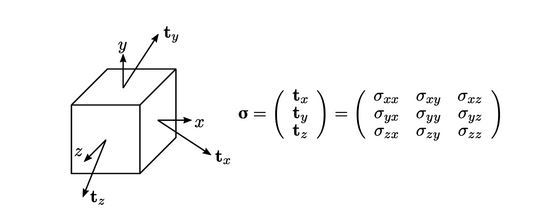
Sebagai gantinya, kita memerlukan 3 vektor tarikan ( 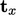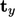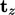$\text{[math]}$ , $\text{[math]}$ , $\text{[math]}$ ) yang didefinisikan dalam bidang-bidang yang saling tegak lurus, yaitu (x, y, z). Hal ini menghasilkan tensor tegangan ( 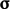$\text{[math]}$ ) dengan 9 komponen yang terdiri dari 3 vektor tarikan, masing-masing mengandung 3 komponen.
Tarikan dapat dihitung pada suatu permukaan dengan orientasi apa pun dengan mengambil hasil kali dalam vektor normal satuan (n) dan tensor tegangan ( 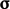$\text{[math]}$ ) sehingga

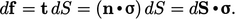df = t dS = (n ☐☐☐)dS = dS ☐☐☐: \relax \special {t4ht=

(2.17)

Tensor

Kita telah mendefinisikan tensor tegangan 3, sebuah entitas dengan 9 nilai komponen, yang sesuai dengan sumbu-sumbu x, y, dan z, kita (atau lebih spesifiknya vektor-vektor dasar berukuran satuan yang sejajar dengan sumbu-sumbu x,y dan z kita).

Sebenarnya, istilah “tensor” menggambarkan entitas apa pun dengan banyak nilai komponen yang sesuai dengan dimensi ruang – disini adalah 3. Sebuah tensor memiliki pangkat r, sehingga jumlah nilai komponen untuk ruang 3D = 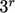$\text{[math]}$ .

Dalam literasi ini, kami menggunakan istilah “tensor” dengan memiliki arti sebagai “tensor pangkat 2” kecuali dinyatakan lain. Sebuah vektor adalah tensor pangkat 1 dan sebuah skalar adalah pangkat 0.

Hasil kali dari suatu vektor (a) dan tensor (T) menghasilkan sebuah vektor yang 3 komponennya dievaluasi sebagai berikut

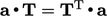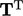Hasil kali tensor ini hanya komutatif jika T simetris karena $\text{[math]}$ – lihat persamaan (2.24) untuk transpose ( $\text{[math]}$ ).