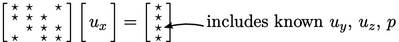EQUATION DISCRETISATION

Diskretisasi persamaan menciptakan sebuah persamaan linear untuk setiap sel. Untuk sel di atas, persamaannya mungkin memiliki bentuk berikut:

Diskritisasi persamaan mengubah persamaan diferensial parsial untuk bidang kontinu , misalnya tekanan 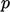$persamaan$ , menjadi himpunan persamaan linier untuk bidang diskrit .

Nilai bidang utama, misalnya 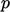$persamaan$ , dikaitkan dengan sel. Bidang kemudian diwakili oleh array nilai,, 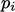$persamaan$ untuk indeks sel 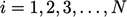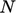$persamaan$ . $persamaan$ adalah jumlah total sel.

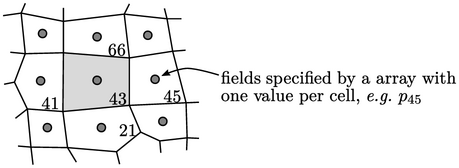
$GAMBAR\santai \khusus {t4ht=$

Diskritisasi persamaan menghasilkan persamaan linier untuk setiap sel. Untuk sel 43 di atas, persamaannya mungkin memiliki bentuk berikut:

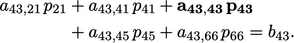
$gambar\santai 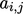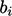\khusus {t4ht=$

di mana $persamaan$ dan $persamaan$ adalah koefisien yang sesuai dengan indeks sel 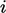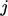$persamaan$ , $persamaan$ (koefisien diagonal dicetak tebal ). Himpunan persamaan linier untuk semua sel dapat dituliskan sebagai persamaan matriks dengan bentuk:

2 32 3 2 3 a1;1 a1;2 a1;3 a1;N p1 b1 66 7766 77 66 77 66 a2;1 a2;2 a2;3 a2;N 7766 p2 77 66 b2 77 66 a3;1 a3;2 a3;3 a3;N 7766 p3 77= 66 b3 77 66 : : : : : 7766 : 77 66 : 77 64 :: :: :: :: :: 7564 :: 75 64 :: 75 aN;1 aN;2 aN;3 aN;N pN bN \relax \special {t4ht=

(3.1)

Matriks berisi sekumpulan koefisien 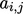$persamaan$ yang setiap barisnya 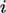$persamaan$ sesuai dengan persamaan linier untuk sel dengan indeks 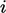$persamaan$ . Setiap baris koefisien bukan nol hanya untuk masing-masing sel (diagonal 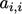$persamaan$ ) dan tetangga dekat. Semua koefisien lainnya adalah nol, sehingga matriks menjadi sangat renggang.

Persamaan matriks dapat direpresentasikan sebagai 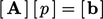$persamaan$ , dimana: 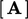$persamaan$ adalah koefisien matriks; 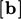$persamaan$ apakah koefisien sumbernya 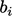$per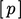samaan$ ; dan, $persamaan$ adalah bidang tekanan yang didiskritisasi. Hal ini juga dapat diilustrasikan sebagai berikut, di mana ‘ $persamaan$ ‘ menunjukkan koefisien bukan nol.

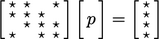? ? ? ? ? ? ? hal = ? ?? ?? ?? ?? \santai \khusus {t4ht=

Solusi terpisah

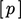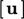
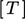
Simulasi CFD umumnya menyelesaikan serangkaian persamaan fisika, misalnya untuk konservasi massa, momentum, dan energi. Metode volume terbatas secara tradisional mendiskritisasi setiap persamaan fisis secara terpisah untuk membentuk persamaan matriks individual untuk variabel solusi tunggal, misalnya ,,, $persamaan$ daripada membuat persamaan matriks tunggal yang mewakili semua persamaan fisis. $persamaan$ $persamaan$

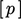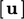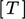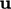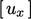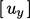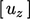Persamaan matriks tersegregasi diselesaikan satu per satu variabel, misalnya menyelesaikan $persamaan$ , $persamaan$ dan $persamaan$ dalam langkah-langkah terpisah. Jika variabel solusinya berupa vektor atau tensor , misalnya $persamaan$ dipisahkanmenjadi persamaan matriks individual untuk setiap komponen, misalnya $persamaan$ , $persamaan$ , $persamaan$ .

Persamaan matriks diselesaikan secara iteratifurutan, di mana persamaan untuk satu variabel, misalnya 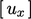$persamaan$ , menggabungkan nilai-nilai saat ini dari variabel lain, misalnya 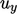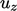$persam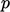aan$ , $persamaan$ dan $persamaan$ , ke dalam vektor sumber, seperti yang ditunjukkan di bawah ini.

$GAMBAR\santai \khusus {t4ht=$