Matrix Construction
Pembangunan setiap persamaan matriks melibatkan pembentukan koefisien matriks dan sumber dari suku dalam persamaan yang sedang diselesaikan, dengan penyesuaian lebih lanjut untuk kondisi batas.
Gambar di bawah ini menggambarkan proses pembangunan persamaan matriks untuk suatu medan 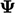 dari suatu persamaan yang mencakup adveksi, diifusi, dan sumber
dari suatu persamaan yang mencakup adveksi, diifusi, dan sumber 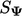 .
.
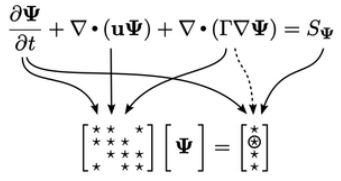
Koefisien untuk matriks 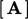 dan sumber
dan sumber 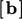 dihitung untuk setiap suku individusi dalam persamaan e.g.
dihitung untuk setiap suku individusi dalam persamaan e.g. 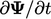 ,
, 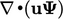 , etc menggunakan metode deksritisasi yang dijelaskan pada bab ini.
, etc menggunakan metode deksritisasi yang dijelaskan pada bab ini.
Koefisien keseluruhan dihitung sebagai jumlah dari koefisien untuk setiap suku dalam persamaan tersebut. Sebagian besar suku memberikan kontribusi baik pada matriks maupun koefisien sumber, meskipun hal ini tergantung pada pilihan skema diskritisasi
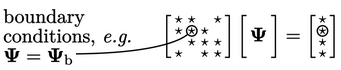
Finally, boundary conditions are incorporated into the equation through further adjustments to coefficients in 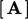 and
and 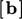 as shown below. The adjustments, principally from the advection and diffusion terms, are applied to coefficients corresponding to cells at the domain boundary.
as shown below. The adjustments, principally from the advection and diffusion terms, are applied to coefficients corresponding to cells at the domain boundary.
Akhirnya, kondisi batas saling bersinggungan ke dalam persamaan melalui pengaturan lebih lanjut pada koefisian 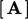 dan
dan 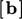 seperti di bawah ini. Pengaturan, prinsipnya dari istilah adveksi dan difusi, yang digunakan pada koefisien yang saling berhubungan pada cell pada domain boundary
seperti di bawah ini. Pengaturan, prinsipnya dari istilah adveksi dan difusi, yang digunakan pada koefisien yang saling berhubungan pada cell pada domain boundary
Implisit dan eksplisit
Persamaan untuk suatu persamaan medan 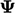 pada halaman sebelumnya didiscretisasi untuk membentuk persamaan matriks
pada halaman sebelumnya didiscretisasi untuk membentuk persamaan matriks 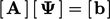 . Diskretisasi disebut implisit ketika ia berkontribusi terhadap koefisien
. Diskretisasi disebut implisit ketika ia berkontribusi terhadap koefisien 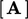 dengan memperlakukan
dengan memperlakukan 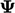 sebagai medan yang terpecahkan
sebagai medan yang terpecahkan 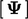 .
.
Diskretisasi eksplisit menghitung koefisien dalam 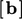 hanya, dengan menggunakan nilai-nilai saat ini dari medan. Ketika memecahkan suatu persamaan untuk
hanya, dengan menggunakan nilai-nilai saat ini dari medan. Ketika memecahkan suatu persamaan untuk 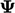 , turunan tanpa persamaan harus eksplisit. Istilah dengan
, turunan tanpa persamaan harus eksplisit. Istilah dengan 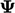 bisa diperlakukan secara eksplisit dengan menggunakan nilai-nilai saat ini dari
bisa diperlakukan secara eksplisit dengan menggunakan nilai-nilai saat ini dari 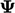 , tetapi umumnya tidak, karena solusi eksplisit tidak stabil melampaui langkah waktu pembatas seperti yang dijelaskan di Bagian 3.17. Sebuah pengecualian yang mencolok dari ini adalah istilah-istilah yang dibahas di Bagian 3.20.
, tetapi umumnya tidak, karena solusi eksplisit tidak stabil melampaui langkah waktu pembatas seperti yang dijelaskan di Bagian 3.17. Sebuah pengecualian yang mencolok dari ini adalah istilah-istilah yang dibahas di Bagian 3.20.
Turunan curl, misalnya  , termasuk istilah dalam
, termasuk istilah dalam 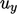 dan
dan 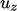 dalam persamaan matriks terpisah untuk
dalam persamaan matriks terpisah untuk 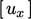 . Istilah-istilah ini harus diperlakukan secara eksplisit karena mereka tidak termasuk
. Istilah-istilah ini harus diperlakukan secara eksplisit karena mereka tidak termasuk 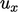 itu sendiri. Situasinya untuk
itu sendiri. Situasinya untuk 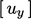 dan
dan 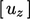 adalah sama, sehingga turunan curl hanya bisa eksplisit.
adalah sama, sehingga turunan curl hanya bisa eksplisit.
Hal ini meninggalkan istilah-istilah berikut yang umumnya diperlakukan secara implisit:
- turunan waktu
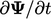 ;
; - difusi (Laplacian)
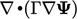 ;
; - adveksi
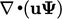 ;
; - fungsi linier implisit
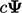 , di mana
, di mana  adalah skalar.
adalah skalar.
Bab ini merincikan: diskretisasi dari istilah-istilah ini, yang umumnya diperlakukan secara implisit; dan, istilah-istilah lain seperti divergensi  dan gradien
dan gradien 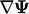 yang hanya bisa didiskritisasi secara eksplisit dalam solusi terpisah.
yang hanya bisa didiskritisasi secara eksplisit dalam solusi terpisah.
Lanjutan
Pilihan metode numerik menentukan bagaimana koefisien 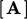 dan
dan 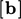 dihitung serta karakteristik persamaan matriks yang dihasilkan
dihitung serta karakteristik persamaan matriks yang dihasilkan 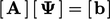 .
.
Metode volume hingga, FVM, yang dijelaskan di sini berakar kuat pada konsep dasar volume kontrol, yang dijelaskan dalam Bagian. 3,1 . Ia menggunakan integral pada permukaan yang mengelilingi volume yang diterapkan pada jerat polihedral tidak beraturan, dijelaskan dalam Bagian. 3.2.
Diskritisasi dijelaskan dalam istilah operator diferensial, misalnya 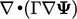 dan
dan 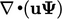 , yang diterapkan pada bidang umum
, yang diterapkan pada bidang umum 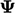 .
.
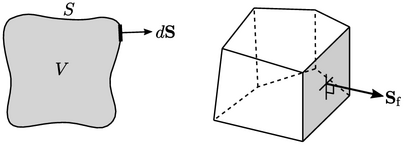
Konsep utamanya adalah bahwa permukaan di dalam jaring membentuk permukaan tertutup yang mengelilingi volume terbatas, misalnya sel tunggal. Integral permukaan apa pun yang mewakili turunan, misalnya  , didekati dengan penjumlahan pada permukaan ‘
, didekati dengan penjumlahan pada permukaan ‘ 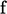 ‘ yang membentuk permukaan, yaitu
‘ yang membentuk permukaan, yaitu
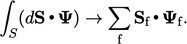 |
Fluks yang terkait dengan 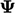 , yaitu
, yaitu 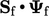 , kemudian harus dihitung. Nilai
, kemudian harus dihitung. Nilai 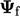 diperlukan pada setiap sisi , yang harus dihitung dengan beberapa metode interpolasinilai dari
diperlukan pada setiap sisi , yang harus dihitung dengan beberapa metode interpolasinilai dari 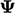 sel yang berdekatan dengan wajah masing-masing.
sel yang berdekatan dengan wajah masing-masing.
Sifat intensif dan ekstensif
Dalam bab ini, turunan dan diskritisasinya dijelaskan pada suatu titik , misalnya 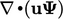 , misalnya Persamaan. (3.8):
, misalnya Persamaan. (3.8):
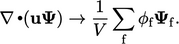 |
Menghitung turunan dengan ekspresi ini menggunakan bidang yang diketahui 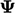 hanya menghasilkan bidang lain (dengan nilai yang ditentukan di pusat sel, dengan satuan
hanya menghasilkan bidang lain (dengan nilai yang ditentukan di pusat sel, dengan satuan 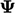 /waktu).
/waktu).
Bidang yang dihasilkan adalah 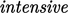 , artinya tidak bergantung pada ukuran sistem/geometri. Seperti bidang intensif lainnya, misalnya
, artinya tidak bergantung pada ukuran sistem/geometri. Seperti bidang intensif lainnya, misalnya 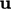 dan
dan 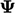 bidang itu sendiri, bidang ini dapat digunakan dalam perhitungan lebih lanjut, misalnya dalam turunan lain atau ditambah/dikurangi dari bidang lain.
bidang itu sendiri, bidang ini dapat digunakan dalam perhitungan lebih lanjut, misalnya dalam turunan lain atau ditambah/dikurangi dari bidang lain.
Properti ekstensif bergantung pada ukuran sistem. Misalnya, fluks volumetrik 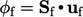 yang dijelaskan dalam Sec. 3.9 tergantung pada area wajah
yang dijelaskan dalam Sec. 3.9 tergantung pada area wajah 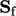 . Operasi numerik yang melibatkan properti ekstensif, misalnya penjumlahan, pengurangan, atau pemetaan ke lokasi lain, umumnya menghasilkan data yang tidak berarti.
. Operasi numerik yang melibatkan properti ekstensif, misalnya penjumlahan, pengurangan, atau pemetaan ke lokasi lain, umumnya menghasilkan data yang tidak berarti.
Meskipun penghitungan turunan menghasilkan bidang intensif, persamaan matriks dibuat dalam bentuk ekstensif , dengan koefisien dan vektor sumber diskalakan berdasarkan volume sel 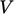 . Dengan kata lain, pada contoh diskritisasi di atas, perkalian dengan
. Dengan kata lain, pada contoh diskritisasi di atas, perkalian dengan 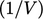 akan dihilangkan.
akan dihilangkan.
Tidak ada 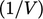 pengali dalam diskritisasi suku-suku yang tidak melibatkan integral permukaan, misalnya turunan waktu Persamaan. (3.21) dan istilah dalam Sec. 3.20. Untuk suku-suku tersebut, penghitungan koefisien dan sumber matriks mencakup perkalian dengan
pengali dalam diskritisasi suku-suku yang tidak melibatkan integral permukaan, misalnya turunan waktu Persamaan. (3.21) dan istilah dalam Sec. 3.20. Untuk suku-suku tersebut, penghitungan koefisien dan sumber matriks mencakup perkalian dengan 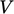 .
.
