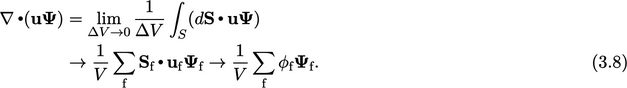Advection Discretisation

Di detik. 2.8, kami mendeskripsikan istilah adveksi sebagai bentuk 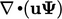atau 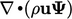. Dimasukkannya kecepatan 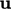dalam divergensi memberikan istilah karakteristik tertentu yang memerlukan perlakuan khusus dalam diskritisasi.

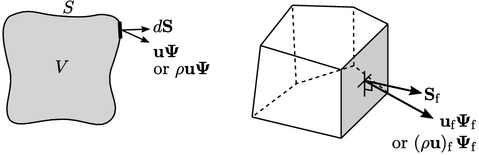
Mengikuti prinsip volume terbatas yang diuraikan dalam Sec. 3.1, diskritisasi mendekati integral permukaan dengan penjumlahan pada permukaannya

Diskritisasi memerlukan perhitungan fluks volumetrik 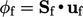(lihat Bagian. 2.3). Dalam hal 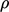termasuk dalam suku adveksi 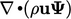, 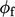adalah fluks massa .

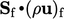Dalam perhitungan fluks, interpolasi dari 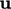pusat sel ke 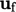permukaan menggunakan skema linier Sec. 3.7. Demikian pula, skema linier digunakan untuk interpolasi .

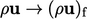Persoalan kritisnya — salah satu yang paling penting dalam numerik CFD — adalah bagaimana mengekspresikan properti adveksi kita 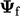dalam bentuk nilai 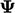di sel yang berdekatan.

Pengenalan skema adveksi

Properti adveksi 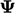diangkut ke arah kecepatan aliran 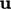. Interpolasi pada permukaan 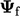biasanya melibatkan arah aliran. Pada grafik di bawah, wajah f diposisikan di antara dua sel. Berdasarkan arah alirannya, sel diberi label melawan arah angin ‘U’ dan melawan arah angin ‘D’.

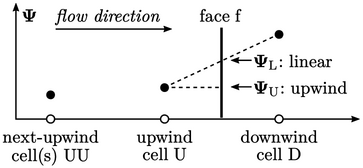
Skema interpolasi linier , ⁵dijelaskan dalam Bagian. 3.7, tidak menggunakan arah aliran tetapi dinyatakan 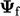dalam sel yang berdekatan. Pada pandangan pertama, pilihan skema ini logis ketika mempertimbangkan akurasi . Namun untuk adveksi, skema linier cenderung menghasilkan solusi tak terbatas yang tidak stabil.

Skema melawan arah angincukup diwakili 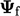oleh nilai di sel melawan arah angin 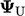. Hal ini masuk akal dari sudut pandang fisik karena partikel-partikel cairan dalam sel yang melawan arah angin ditakdirkan untuk melakukan perjalanan ke permukaan, membawa properti 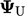bersamanya.⁶

Meskipun skema linier umumnya tidak terbatas, skema melawan arah angin menunjukkan akurasi yang buruk. Pada bagian berikut kita mengeksplorasi perilaku melawan arah angin sebelum melihat skema yang menawarkan akurasi lebih besar sambil mencoba mempertahankan batasan.