BOUNDARY LAYERS
Boundary layers. Lapisan batas adalah wilayah fluida yang terbentuk di sepanjang batas padat di mana kecepatan u bervariasi: dari nol di sepanjang batas (kondisi no-slip, Bagian 4.4); hingga nilai yang sebagian besar tidak terpengaruh oleh kedekatan batas, ditentukan oleh kondisi aliran.
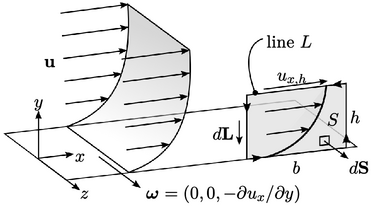
Gambar di atas menunjukkan lapisan batas untuk aliran pada persamaan 𝜒 arah dengan kecepatan 𝜐(𝑦1), sepanjang batas padat datar yang berorientasi pada arah normal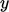 
. Pada permukaan batas, vortisitas 
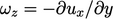signifikan.
Vortisitas dapat ditunjukkan di bagian datar dari lapisan batas dengan lebar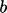 
dan tinggi 
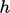(di atas, kanan). Dengan menerapkan teorema Stokes, Persamaan (2.39), integral =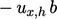 
sepanjang garis atas (dengan nilai nol di sepanjang dinding dan sisi vertikal). Rata-rata vortisitas di atas area datar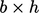 
adalah 
.
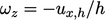Lapisan batas adalah sumber utama vortisitas bagi turbulensi. Turbulensi terjadi ketika ketidakstabilan, misalnya yang diinduksi oleh kasar halusnya permukaan batas, menyebabkan vortisitas menjadi kacau, dipertahankan oleh kecepatan yang cukup tinggi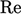 
.
Pertumbuhan lapisan batas berkaitan dengan transportasi vortisitas. Pada aliran di atas pelat datar, vortisitas yang dihasilkan di tepi depan diadvetkan oleh aliran, sementara juga difusi menjauh dari pelat.
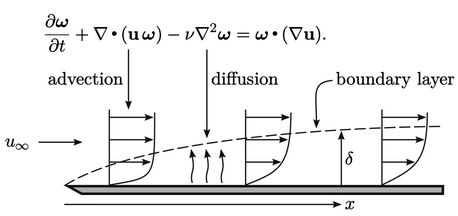
Vortisitas menjalar melalui difusi sejauh jarak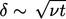 
dalam waktu 𝔱, lihat Bagian 2.22. Dalam waktu tersebut, vortisitas di advetkan sejauh jarak 
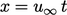, di mana 
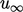adalah kecepatan aliran freestream. Jika dibandingkan dengan jarak yang sama selama waktu yang sama 𝔱, ketebalan lapisan batas adalah
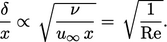 | (6.6) |
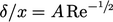cocok untuk lapisan batas laminar, dengan koefisien Α tergantung pada definisi dari 𝛿. Data dan analisis, termasuk contohnya solusi Blasius, menunjukkan 
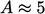dalam kasus "ketebalan 99%", yaitu jarak dari dinding di mana kecepatan mencapai 99% dari nilai asimtotiknya.