diskritisasi adveksi yang dibatasi
Diskritisasi Adveksi yang Dibatasi. Section 2.9 menjelaskan sifat-sifat konservasi dan terbatas dari turunan adveksi persamaan 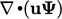 dan
dan 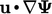 , masing-masing. Menurut persamaan (2.31), istilah-istilah tersebut setara ketika
, masing-masing. Menurut persamaan (2.31), istilah-istilah tersebut setara ketika 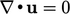 , yaitu ketika persamaan konservasi massa Eq. (2.8) terpenuhi dalam kasus ketika
, yaitu ketika persamaan konservasi massa Eq. (2.8) terpenuhi dalam kasus ketika 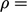 konstan.
konstan.
Selama perhitungan aliran tak dapat dipadatkan, kesalahan numerik dapat signifikan, terutama pada awal perhitungan keadaan tunak. Persamaan pengatur tidak terpenuhi, termasuk konservasi massa, sehingga 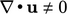 .
.
Diskritisasi suatu suku adveksi yang memiliki bentuk persamaan 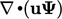 seperti yang dijelaskan dalam Bagian 3.9 dapat menyebabkan ketidakterbatasan pada
seperti yang dijelaskan dalam Bagian 3.9 dapat menyebabkan ketidakterbatasan pada 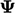 . Jika
. Jika 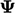 memiliki batasan fisik yang dilanggar, solusi dengan cepat menjadi tidak stabil.
memiliki batasan fisik yang dilanggar, solusi dengan cepat menjadi tidak stabil.
Penambahan istilah 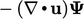 memastikan keterbatasan, sementara
memastikan keterbatasan, sementara 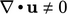 , dengan pengorbanan pada konservasi. Begitu
, dengan pengorbanan pada konservasi. Begitu 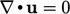 , solusi tersebut menjadi terbatas dan konservatif.
, solusi tersebut menjadi terbatas dan konservatif.
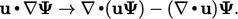 | (3.43) |
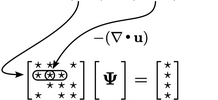
Istilah tambahan ini bersifat implisit dalam 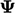 , sehingga memberikan kontribusi
, sehingga memberikan kontribusi 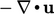 ke koefisien diagonal matriks, Jika
ke koefisien diagonal matriks, Jika 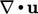 positif, kita mungkin mengharapkan matriks singular, seperti dibahas dalam bagian 3.20. Namun, penurunan koefisien diagonal seimbang dengan peningkatan dari diskritisasi
positif, kita mungkin mengharapkan matriks singular, seperti dibahas dalam bagian 3.20. Namun, penurunan koefisien diagonal seimbang dengan peningkatan dari diskritisasi 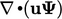 . Jika istilah tersebut menggunakan skema upwind, diskritisasi dapat dibagi menjadi kontribusi dari aliran keluar positif
. Jika istilah tersebut menggunakan skema upwind, diskritisasi dapat dibagi menjadi kontribusi dari aliran keluar positif 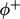 dan aliran masuk negatif
dan aliran masuk negatif 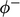 .
.
Dalam bentuk ekstensif (yaitu, disesuaikan dengan 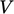 , lihat bagian 3.24, menggunakan nilai dalam sel yang diminati
, lihat bagian 3.24, menggunakan nilai dalam sel yang diminati 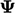 dan sel tetangga
dan sel tetangga 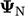 , istilah-istilahnya adalah :
, istilah-istilahnya adalah :
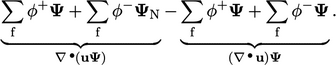 |
Istilah-istilah 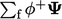 saling meniadakan, meninggalkan koefisien negatif untuk sel tetangga (karena
saling meniadakan, meninggalkan koefisien negatif untuk sel tetangga (karena 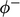 bersifat negatif). Koefisien diagonal kemudian sama dengan jumlah besaran dari koefisien sel tetangga tersebut, menghasilkan matriks yang dapat diinversi.
bersifat negatif). Koefisien diagonal kemudian sama dengan jumlah besaran dari koefisien sel tetangga tersebut, menghasilkan matriks yang dapat diinversi.
Fenomena Fisika
Keterbatasan dan konservasi dapat dikompromikan ketika suatu istilah dalam suatu persamaan tidak mencerminkan fisika dari masalah tersebut. Sebagai contoh, dalam pemodelan pembakaran kecepatan nyala, digunakan suatu parameter b yang mewakili fraksi cam[uran bahan bakar yang belum terbakar.
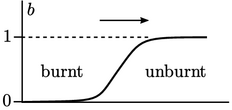
Persamaan untuk 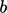 mencakup istilah sumber
mencakup istilah sumber 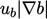 , di mana
, di mana 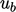 adalah kecepatan nyala yang dihitung. Penambahannya dapat menyebabkan solusi
adalah kecepatan nyala yang dihitung. Penambahannya dapat menyebabkan solusi 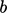 jatuh di bawah batas bawahnya, yaitu 0.
jatuh di bawah batas bawahnya, yaitu 0.
Dengan mengalikan dan membagi dengan 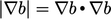 , istilah tersebut berubah menjadi
, istilah tersebut berubah menjadi 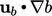 , di mana
, di mana 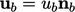 dan unit vektor
dan unit vektor 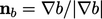 . Dalam bentuk ini, istilah tersebut merepresentasikan adveksi non-konservatif dari
. Dalam bentuk ini, istilah tersebut merepresentasikan adveksi non-konservatif dari 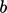 oleh kecepatan nyala
oleh kecepatan nyala 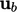
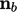 , yang mencermati sifat fisik dari pembakaran. Keterbatasan dapat dipertahankan dengan pemilihan yang sesuai dari skema adveksi.
, yang mencermati sifat fisik dari pembakaran. Keterbatasan dapat dipertahankan dengan pemilihan yang sesuai dari skema adveksi.
