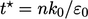Turbulent Dissipation Rate
Sebuah model lengkap untuk π£t masih diperlukan untuk menyelesaikan persamaan momentum yang dirata-ratakan ensemble, misalnya Persamaan (6.26). Diskusi di Bagian 6.11 menunjukkan bahwa π£t adalah hasil kali dari π’m dan πm, memerlukan dua model untuk merepresentasikan setiap skala. Karena π’m πΌπ1β2, π dapat merepresentasikan skala kecepatan, dimodelkan oleh Persamaan (6.28).
Laju dissipasi turbulen π sesuai dengan laju transfer energi kinetik ke bawah tangga energi ~π’3/π, seperti yang dibahas di Bagian 6.6. Hal ini berlaku untuk semua skala turbulen termasuk skala panjang pencampuran yang lebih besar, sehingga ππΌπ3β2 /πm. Dengan mensubstitusi ekspresi π’m dan πm ke dalam π£t = π’m πm menghasilkan viskositas turbulen
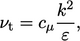 | (6.31) |
di mana πΆπ adalah sebuah konstanta. Dari data empiris, ππ = 0.09, kecuali di dalam lapisan viskos dan lapisan buffer dekat dinding, lihat Bagian 74.
Transport Turbulent Dissipation Rate
Saat ini diperlukan sebuah model untuk π , baik untuk menghitung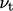 
melalui Persamaan (6.31) maupun untuk memberikan variabel yang tersisa dalam Persamaan (6.28). Model dapat diberikan melalui persamaan transportasi untuk π
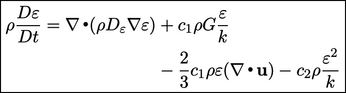 | (6.32) |
di mana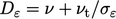 
adalah difusi molekuler dan turbulen yang digabungkan dengan koefisien yang dapat disesuaikan ππ, biasanya diatur menjadi 1.3. Koefisien sisa dan disesuaikan untuk menangkap perilaku berbagai aliran.
Persamaan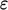 
-equation, Persamaan (6.32), dapat diperoleh dalam hal sifat statistik, menggantikan suku-suku orde tinggi dalam π’' ( dengan model-model dengan koefisien πΆ1, πΆ2.
Atau, dapat diperoleh dengan mengalikan variabel utama, π atau π,dalam setiap suku dari Persamaan (6.28) dengan πβπdan memperkenalkan koefisien π, π1, dan π2.
Bagian π1ππΊπ/π dalam Persamaan (6.32) menyebabkan meningkat dengan πΊ. Ini logis karena turbulensi yang dihasilkan bergerak ke bawah tangga energi, sehingga pada akhirnya mempengaruhi laju disipasi.
Sementara bagian πΆ2ππ2/πΎdapat dibenarkan dengan mempertimbangkan dekay bebas turbulensi. Jika cairan berhenti bergerak (π’ = 0) dan turbulensi tidak lagi dihasilkan (πΊ = 0), maka (dengan asumsi konstan π dan mengabaikan difusi) Persamaan (6.28) dan Persamaan (6.32) disederhanakan menjadi
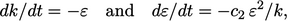 | (6.33) |
masing-masing. Mengintegrasikan persamaan-persamaan yang digabungkan menghasilkan πβπ0 = (π/π+)c2, di mana subskrip "0" menunjukkan nilai awal.
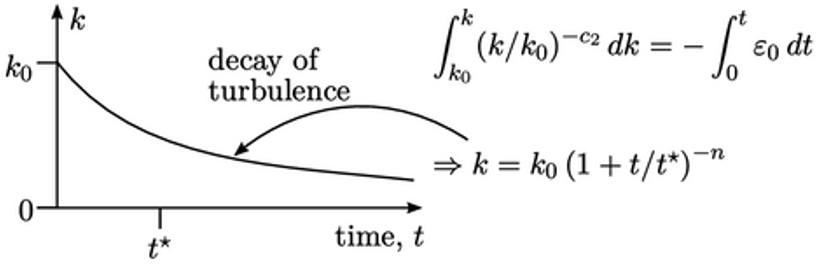
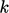seiring waktu ke daya dan skala waktu 
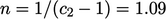dan 