Incompressible

Kita dapat mendapatkan serangkaian persamaan untuk aliran yang tak dapat dimampatkan (incompressible flow) yang meliputi:

Konservasi massa, Pers. (2.8);
Konservasi momentum, Pers. (2.19);
Turunan materi untuk u, Pers. (2.26);
Tensor laju deformasi, Pers. (2.33);
Model fluida Newtonian, Pers. (2.41).

Menggabungkan Pers. (2.41) dan Pers. (2.33) serta menggunakan Pers. (2.36) untuk bagian deviatorik dari sebuah tensor, memberikan suatu ungkapan untuk tegangan:

Substitusi 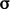ke dalam pers. (2.19) dan menerapkan pers. (2.26) memberikan sebuah persamaan untuk momentum bagi fluida Newtonian :

Pembentukan persamaan di atas menggunakan pers. (2.35) dan identitas 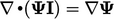$\text{[math]}$ pada halaman 84
Sebuah fluida incompressible menunjukkan 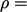$\text{[math]}$ konstan dari waktu ke waktu, yaitu untuk volume bergerak dari fluida 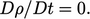$\text{[math]}$ Menggabungkan turunan materi pers. (2.14) dan konservasi massa pers. (2.8) memberikan 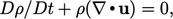$\text{[math]}$ yang menghasilkan kondisi tak dapat dimampatkan.

Sebuah material homogen tak dapat dimampatkan menunjukkan 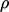$\text{[math]}$ = konstan secara seragam di seluruh fluida. Dengan asumsi tersebut, pada pers. (2.45) dapat ditulis sebagai bberikut:

Ini adalah persamaan momentum untuk fluida Newtonian homogen, incompressible. Ini termasuk : viskositas kinematik 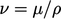$\text{[math]}$ dalam satuan SI dari 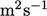$\text{[math]}$ dan p mewakili tekanan kinematik, yaitu dibagi oleh p, dalam satuan SI dari $\text{[math]}$ .
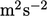Identitas 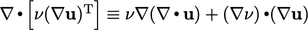$\text{[math]}$ dan pers. (2,46) menghasilkan istilah-istilah dalam pers. (2.47).

Konservasi massa dan momentum, yang direpresentasikan oleh persamaan (2.46) dan persaman (2.47) secara berturut-turut, memberikan dua persamaan-satu persamaan skalar, satu persamaan vektor- untuk dua bidang, p dan u. Namun, persamaan (2.46) tidak dapat diselesaikan sendiri karena hanya memberikan satu persamaan untuk vektor u yang berisi 3 komponen.
Sebuah persamaan skalar, yang mencakup baik p maupun u, dapat diperoleh dengan mengambil divergensi dari persamaan (2.47) dan mengeliminasi suku-suku dengan mensubstitusikan persamaan (2.46), dengan catatan bahwa 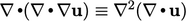$\text{[math]}$ . Untuk v dan b yang konstan dan seragam, persamaannya adalah :

Persamaan tekanan ini dapat menggantikan Persamaan (2.46) untuk memberikan sepasang persamaan, dengan Persamaan (2.47), untuk kedua p dan u. Bab 5 menjelaskan algoritma yang digunakan dalam metode volume hingga yang menghubungkan kedua persamaan menggunakan bentuk modifikasi dari Persamaan (2.48).