Perhitungan yang dihitung

Pengantar konstruksi matriks, Sec. 3.5, menjelaskan diskritisasi suku-suku secara implisit dan eksplisit dalam suatu persamaan. Disimpulkan bahwa turunan utama dari 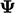$persamaan$ hal tersebut dapat diperlakukan secara implisit — membentuk koefisien matriks dalam 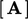$persamaan$ — adalah turunan waktu, adveksi, dan Laplacian.

Suku dengan turunan lainnya harus dihitung dari masing-masing bidang, misalnya 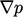$persamaan$ dari nilai saat ini sebesar 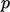$persamaan$ . Di detik. 3.15, kami telah menjelaskan diskritisasi gradien, yang selalu eksplisit. Bagian ini mengumpulkan turunan lain yang ditemukan dalam persamaan dinamika fluida dan model terkait.

Istilah Divergensi Umum

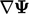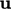Suku divergensi umum adalah suku apa pun yang dapat diwakili oleh $persamaan$ . Ini tidak termasuk istilah Laplacian yang mencakup gradien $persamaan$ , dan adveksi yang mencakup $persamaan$ .

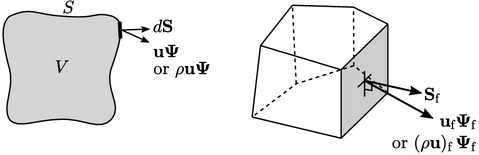
Diskritisasi istilah divergensi umum adalah penghitungan eksplisit menggunakan nilai saat ini 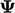$persamaan$ . Hal ini didasarkan pada integral permukaan menggunakan definisi divergensi di Sec. 2.23 seperti yang ditunjukkan di bawah ini:

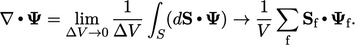Z -1-- 1-X r = liVm!0 V S(dS ) ! V Sf f: f \relax \special {t4ht=

(3.30)

Nilai nominal 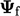$persamaan$ umumnya diinterpolasi dari nilai sel menggunakan skema linier. Istilah-istilah yang didiskritisasi menggunakan skema ini termasuk 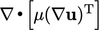$persamaan$ dalam Persamaan. (2.45), perbedaan stres $persamaan$ , dll.

Curl Sebuah Vektor

Turunan ikal $persamaan$ dihitung dari gradien 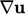$persamaan$ dan menerapkan operator ganda Hodge yang diberikan oleh Persamaan. (2.40) menggunakan relasi berikut:

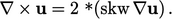r u = 2 (skw ru) : \relax \special {t4ht=

(3.31)

Dengan kata lain, 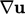$persamaan$ didiskritisasi menurut skema dari Sec. 3.15, dari mana $persamaan$ dihitung dengan Persamaan. (3.31).

Gradient Mag-Square

Turunan yang muncul dalam beberapa persamaan model adalah 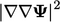, digambarkan sebagai “mag-square grad-grad”. Turunan ini mengembalikan skalar karena mag-square, misalnya 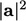, mewakili hasil kali dalam 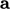dengan dirinya sendiri, seperti yang ditunjukkan pada Persamaan. (2.7).

Perhitungan mag-square selalu menggunakan hasil kali dalam yang sesuai untuk mereduksi hasilnya menjadi skalar. Untuk tensor 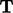, ini adalah hasil kali dalam ganda, yaitu .

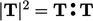Operator lulusan-sarjana 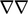menghasilkan tensor peringkat ketiga dalam kasus yang 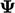merupakan bidang vektor. Untuk menghindari penyimpanan tensor peringkat ketiga, operator grad-grad mag-square dievaluasi dengan menjumlahkan hasil dari operator pada setiap komponen 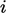oleh

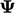
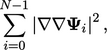$N X 1 jrr ij2 ; i=0 \relax \special {t4ht=$ (3.32)

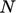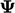dimana $persamaan$ adalah jumlah komponen dalam $persamaan$ .