4.4 Batasan Dinding (Wall Boundaries)

Batasan dinding. Tidak licin Kondisi ini umumnya diterapkan pada dinding kokoh yang kedap air (asumsi 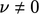$persamaan$ ). Syaratnya adalah 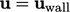$persamaan$ , dimana 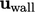$persamaan$ adalah kecepatan dinding, yang biasanya stasioner dengan 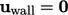$persamaan$ . Bukti di balik kondisi tanpa selip adalah bahwa kondisi ini memprediksi penurunan tekanan di sepanjang tabung berdiameter kecil yang sesuai dengan eksperimen.

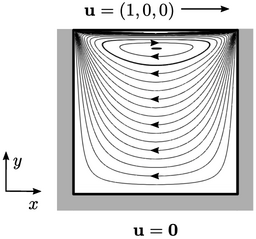
Rongga 2D yang digerakkan oleh tutupadalah permasalahan aliran yang menerapkan kondisi tanpa slip pada seluruh batasnya. Ini memberikan wawasan tentang kondisi batas di 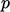$persamaan$ dinding. Dari Persamaan. (2.47) untuk fluida yang tidak dapat dimampatkan, dengan 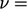$persamaan$ konstan, komponen normal terhadap batas domain adalah

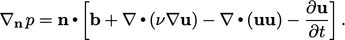@u rn p = n b + r ( ru) r (uu) -@t : \relax \special {t4ht=

(4.4)

Pada batas dinding padat, 2 suku terakhir pada Persamaan. (4.4) menghilang sejak 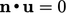$persamaan$ , mengurangi kondisi gradien menjadi

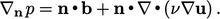rn p = n b + n r ( ru) : \relax \special {t4ht=

(4.5)

Suku kedua dapat ditulis ( 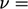$persamaan$ konstanta) 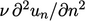$persamaan$ , jadi hanya bukan nol jika terdapat aliran normal terhadap batas di sekitarnya, misalnya di sudut rongga pada contoh kita. Istilahnya biasanya kecil dan perhitungannya melibatkan ekstrapolasi dari solusi internal yang seringkali menimbulkan ketidakstabilan, sehingga umumnya diabaikan.

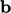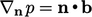Sebuah kekuatan tubuh $persamaan$ , misalnya gravitasi, umumnya ditentukan agar tidak menimbulkan ketidakstabilan. Jika signifikan, maka harus dimasukkan dalam kondisi batas, yaitu $persamaan$ .

Jika tidak, jika tidak ada gaya benda, kita mencapai bentuk standar kondisi batas tekanan pada dinding, 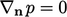$persamaan$ .

Memperbaiki tekanan

Dengan hanya kondisi gradien tekanan pada batas yang tetap , nilai tekanan tidak tetap pada titik mana pun dalam domain solusi. Solusinya tidak unik, seperti yang ditunjukkan pada contoh 1D di bawah dengan kondisi gradien di kedua ujungnya.

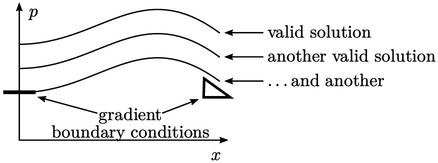
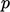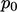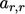Untuk mencapai solusi yang unik, $persamaan$ maka harus ditetapkan ke nilai referensi $persamaan$ pada sel referensi $persamaan$ dalam domain. Untuk mencapai hal ini, koefisien diagonal $persamaan$ digandakan dan 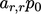$persamaan$ ditambahkan ke sumber 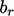$persamaan$ , dalam persamaan matriks 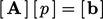$persamaan$ yang dijelaskan oleh Persamaan. (3.1). Perubahan minimal ini “menyematkan” solusi ke $persamaan$ dalam sel $persamaan$ .