Region of influence

Perhitungan CFD dilakukan dengan menyelesaikan persamaan diferensial parsial, seperti untuk kekekalan massa, momentum, dan energi pada domain solusi. Hal ini memerlukan kondisi batas yang sesuai, dibahas dalam Bab 4.

Penyelesaiannya dipengaruhi oleh perubahan apa pun pada nilai bidang, misalnya pada 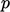$persamaan$ titik tertentu dalam domain, seperti pada batas saluran masuk. Bentuk persamaan menentukan cara perubahan atau gangguan ini, menyebar ke seluruh domain seiring waktu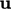 $persamaan$ $persamaan$ .

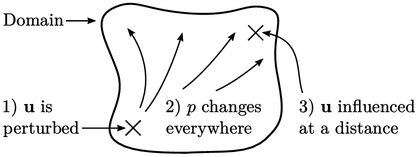
Momentum dan kekekalan massa untuk fluida yang tidak dapat dimampatkan dapat dinyatakan dengan Persamaan (2.67) dan Persamaan (2.48). Bentuk Persamaan (2.48), yang hanya menyertakan turunan Laplacian 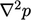$persamaan$ , memastikan bahwa $persamaan$ semua titik dalam domain dipengaruhi secara instan oleh gangguan di $persamaan$ titik mana pun.

Perubahan sesaat yang dihasilkan 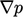$persamaan$ kemudian menyebabkan 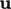$persamaan$ didistribusikan kembali ke mana-mana oleh Persamaan (2.67), dengan perubahan jangka pendek lebih lanjut akibat adveksi dan difusi (dibahas selanjutnya).

Hasil dari fluida yang tidak dapat dimampatkan adalah bahwa 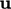$persamaan$ fluida tersebut dipengaruhi secara seketika di mana pun dalam domain tersebut oleh gangguan pada titik mana pun. Dengan kata lain, kecepatan suara $persamaan$ , yang berhubungan dengan perambatan gangguan adalah tak terhingga.

Persamaan adveksi-difusi

Konservasi energi dapat diwakili oleh Persamaan (2.65), di mana gangguan merambat dengan kecepatan karakteristik akibat adveksi dan difusi.

Adveksi merambat dengan kecepatan 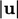$persamaan$ , dengan wilayah pengaruh 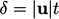$persamaan$ searah aliran. Hubungan tersebut dapat diperoleh dari kemiripan skala bila 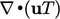$persam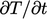aan$ dan $persamaan$ besarannya serupa, yaitu 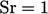$persamaan$ pada Persamaan. (2.69).

Dengan argumen yang sama, wilayah pengaruh difusi sama besarnya 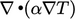$persam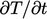aan$ dan $persamaan$ serupa, yakni 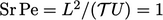$persamaan$ . Difusi “depan” menempuh jarak menurut 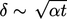$persamaan$ ( $persamaan$ berarti “urutan besarnya”).

Persamaan difusi 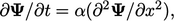$persamaan$ dalam satu dimensi ( 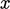$persamaan$ ) mempunyai penyelesaian 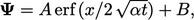$persamaan$ dimana 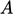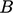$persamaan$ , $persamaan$ adalah konstanta dan 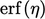$persamaan$ merupakan fungsi kesalahan di bawah ini.

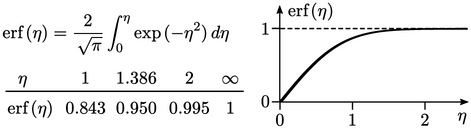
Artinya untuk soal konduksi panas, misalnya pada benda padat, jarak yang ditempuh muka termal adalah 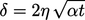$persamaan$ , sesuai dengan argumen kesamaan di atas.

Koefisiennya 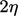$persamaan$ bergantung pada letak bagian 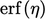$persamaan$ depan kurva. Salah satu opsinya adalah 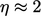$persamaan$ , yang solusinya berada dalam 0,5% asimtot 1.