Limited Advection Schemes

Limited Advection Schemes. Skema alternatif untuk adveksi berupaya mengatasi masalah keterbatasan dan keakuratan skema linier dan melawan arah angin. Banyak skema menerapkan pembatas 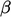$persamaan$ antara 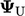$persamaan$ dari melawan arah angin dan 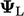$persamaan$ dari skema linier Persamaan. (3.4) berdasarkan

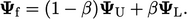f = (1 ) U + L: \relax \special {t4ht=

(3.11)

Ketika 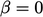$persamaan$ , skema direduksi menjadi melawan arah angin dan menjadi interpolasi linier ketika 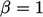$persamaan$ . Untuk mesh seragam ( 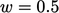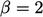$persamaan$ ), $persamaan$ mewakili interpolasi menggunakan nilai sel melawan arah angin.

Skema terbatas berupaya untuk mengoptimalkan 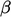$persamaan$ pada setiap sisi, berdasarkan lokal 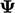$persamaan$ , untuk memaksimalkan akurasi sambil mempertahankan batasan.

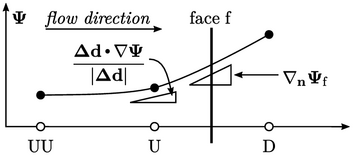
$GAMBAR\santai \khusus {t4ht=$

Banyak skema menganalisis perubahan gradien 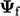$persamaan$ antara sel muka dan sel melawan arah angin dalam arah 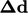$persamaan$ yang menghubungkan pusat sel. Mereka mendefinisikan fungsi rasio $persamaan$ gradien berurutan sebagai:

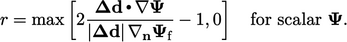r = max 2 -d---r----- 1;0 for scalar : j djrn f \relax \special {t4ht=

(3.12)

Ada banyak skema yang diterbitkan yang mendefinisikan limiter 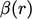$persamaan$ sebagai fungsi rasio gradien $persamaan$ . Skema yang paling berguna dijelaskan pada bagian berikut.

Skema pengurangan variasi total

Banyak skema berguna yang termasuk dalam kelas yang dikenal sebagai Total Variation Diminishing (TVD).⁷Ide TVD adalah jika variasi total bidang 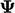$persamaan$ tidak bertambah seiring berjalannya waktu, “melampaui batas” dan osilasi yang terkait dengan ketidakterbatasan tidak akan terjadi.

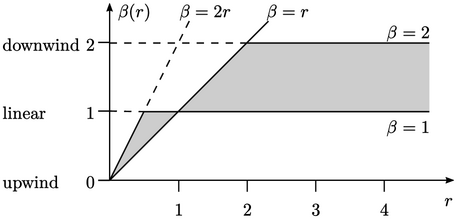
$GAMBAR\santai \khusus {t4ht=$

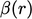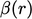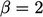Untuk memenuhi syarat sebagai TVD, fungsi pembatas $persamaan$ harus berada dalam area yang diarsir dalam diagram Sweby (di atas).⁸Konsep TVD adalah analisis 1D. Untuk 3DCFD pada jerat polihedral tidak beraturan, osilasi lebih mungkin terjadi pada skema TVD yang $persamaan$ fungsinya cenderung melawan arah angin secara signifikan, yaitu ke arah bagian atas area yang diarsir dekat $persamaan$ .

Sifat selanjutnya dari skema terbatas adalah simetri . Suatu skema dikatakan simetris jika kondisinya 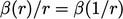$persamaan$ terpenuhi. Ketika hal ini terjadi, skema menerapkan pembatas yang sama pada gradien 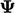$persamaan$ , terlepas dari tanda gradiennya. Sebagai konsekuensinya, sebuah properti 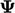$persamaan$ , yang diinisialisasi dengan profil simetris, misalnya kurva lonceng, akan mempertahankan simetrinya di bawah adveksi.