MOdel k-epsilon resolusi rendah
Ada banyak 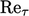 model turbulensi rendah untuk simulasi CFD dimana sel di dekat dinding padat cukup tipis untuk menyelesaikan aliran melalui sub-lapisan kental.
model turbulensi rendah untuk simulasi CFD dimana sel di dekat dinding padat cukup tipis untuk menyelesaikan aliran melalui sub-lapisan kental.
Diantaranya adalah beberapa 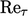
 model rendah berdasarkan Persamaan. (7.1) dan Persamaan. (7.2) dengan tambahan koreksi
model rendah berdasarkan Persamaan. (7.1) dan Persamaan. (7.2) dengan tambahan koreksi 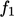 ,
, 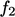 ,
, 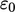 dan
dan 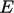 :
:
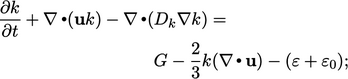 |
(7.29) |
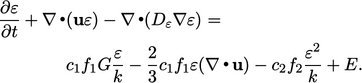 |
(7.30) |
Perhitungan 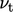 juga mencakup koreksi
juga mencakup koreksi 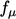 :
:
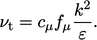 |
(7.31) |
Model ini pertama kali dipresentasikan oleh Jones dan Launder dalam publikasi penting mereka  .12Mereka mengusulkan fungsi untuk
.12Mereka mengusulkan fungsi untuk 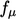 ,
, 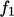 ,
, 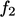 ,
, 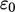 dan
dan 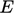 , serta koefisien
, serta koefisien 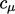 ,
, 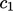 dan
dan 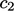 .
.
Launder dan Sharma kemudian mempresentasikannya13 model dengan fungsi yang dimodifikasi 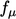 dan koefisien yang lebih mapan yang tercantum dalam Persamaan. (7.3).
dan koefisien yang lebih mapan yang tercantum dalam Persamaan. (7.3).
Model yang dihasilkan dikenal sebagai  model Launder-Sharma.14Ini bisa dibilang model rendah paling populer
model Launder-Sharma.14Ini bisa dibilang model rendah paling populer 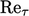 saat ini.
saat ini.
Modifikasi penting pertama pada  model standar adalah
model standar adalah 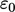 (kadang-kadang dilambangkan dengan “
(kadang-kadang dilambangkan dengan “ 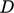 ”) dalam Persamaan. (7.29). Ini adalah laju disipasi di dinding (
”) dalam Persamaan. (7.29). Ini adalah laju disipasi di dinding ( 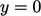 ), lihat gambar, Bagian. 7.7, dihitung oleh
), lihat gambar, Bagian. 7.7, dihitung oleh
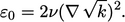 |
(7.32) |
Istilah ini setara dengan 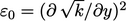 lapisan batas yang konsisten dengan Persamaan. (7.28). Keuntungan dari mendefinisikan ulang laju disipasi adalah
lapisan batas yang konsisten dengan Persamaan. (7.28). Keuntungan dari mendefinisikan ulang laju disipasi adalah 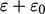 bahwa kondisi batas pada dinding untuk model Launder-Sharma adalah sama untuk
bahwa kondisi batas pada dinding untuk model Launder-Sharma adalah sama untuk 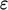 dan
dan 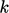 :
:
- nilai tetap
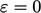 ;
; - nilai tetap
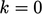 .
.
Modifikasi penting berikutnya adalah 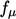 fungsinya
fungsinya
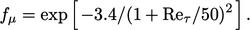 |
(7.33) |
Modifikasi ini mengakui bahwa 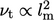 penurunan
penurunan 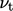 melalui penyangga dan sub-lapisan kental ke dinding, konsisten dengan penurunan
melalui penyangga dan sub-lapisan kental ke dinding, konsisten dengan penurunan  menurut model van Dries Eq. (7.12).
menurut model van Dries Eq. (7.12).
Istilah tambahan 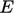 dalam Persamaan. (7.30) adalah sebagai berikut, dirancang agar
dalam Persamaan. (7.30) adalah sebagai berikut, dirancang agar 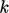 sesuai dengan nilai puncak yang dikenali dalam lapisan buffer:
sesuai dengan nilai puncak yang dikenali dalam lapisan buffer:
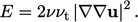 |
(7.34) |
Terakhir, 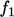 dan
dan 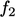 berikan redaman suku produksi dan disipasi dekat dinding pada Persamaan. (7.30).Fungsi standarnya adalah
berikan redaman suku produksi dan disipasi dekat dinding pada Persamaan. (7.30).Fungsi standarnya adalah 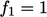 ( yaitu tanpa redaman), dan
( yaitu tanpa redaman), dan
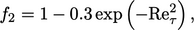 |
(7.35) |
yang memberi 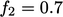 di dinding.
di dinding.
