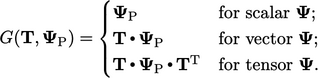4.11 transform condition
Beberapa kondisi batas direpresentasikan 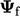 pada batas sebagai transformasi nilai sel
pada batas sebagai transformasi nilai sel 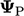 . Mereka dapat dinyatakan dalam kondisi transformasi umum
. Mereka dapat dinyatakan dalam kondisi transformasi umum
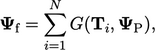 | (4.13) |
Jika 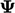 merupakan skalar, kondisi transformasinya setara dengan kondisi gradien nol. Jika tidak, hal ini diimplementasikan sehingga ketentuan dalam
merupakan skalar, kondisi transformasinya setara dengan kondisi gradien nol. Jika tidak, hal ini diimplementasikan sehingga ketentuan dalam 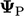 Persamaan. (4.13) berkontribusi pada koefisien dalam
Persamaan. (4.13) berkontribusi pada koefisien dalam 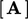 . Kontribusi ini bersifat implisit yang meningkatkan konvergensi ketika menyelesaikan persamaan matriks
. Kontribusi ini bersifat implisit yang meningkatkan konvergensi ketika menyelesaikan persamaan matriks 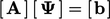 .
.
Sebuah faktor 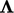 diperkenalkan untuk menentukan kontribusi terhadap koefisien internal. Ini mewakili koefisien internal tunggal untuk setiap komponen
diperkenalkan untuk menentukan kontribusi terhadap koefisien internal. Ini mewakili koefisien internal tunggal untuk setiap komponen 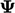 sehingga memiliki peringkat yang sama sebagai
sehingga memiliki peringkat yang sama sebagai 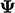 , yaitu suatu vektor bila
, yaitu suatu vektor bila 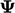 merupakan vektor, dan suatu tensor bila
merupakan vektor, dan suatu tensor bila 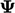 merupakan tensor.
merupakan tensor.
Perkalian setiap koefisien 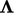 dengan masing-masing komponennya
dengan masing-masing komponennya 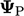 dilambangkan dengan
dilambangkan dengan 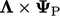 . Dalam kasus vektor
. Dalam kasus vektor 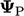 , “perkalian komponen” ini adalah
, “perkalian komponen” ini adalah
Untuk diskritisasi adveksi, nilai nominal direpresentasikan sebagai
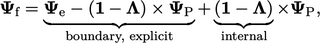 | (4.15) |
dimana 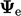 adalah nilai batas eksplisit, dihitung dari ekspresi dalam Persamaan. (4.13) menggunakan nilai saat ini
adalah nilai batas eksplisit, dihitung dari ekspresi dalam Persamaan. (4.13) menggunakan nilai saat ini 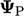 . Istilah eksplisit lainnya menggunakan arus
. Istilah eksplisit lainnya menggunakan arus 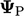 dengan “
dengan “ 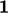 ” yang menunjukkan
” yang menunjukkan 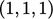 vektor
vektor 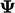 dan
dan 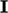 tensor.
tensor.
Diskritisasi Laplacian memerlukan gradien wajah yang normal 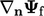 . Menggabungkan
. Menggabungkan 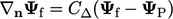 dengan Persamaan. (4.15) memberi
dengan Persamaan. (4.15) memberi
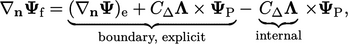 | (4.16) |
di mana gradien eksplisit dihitung
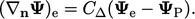 | (4.17) |
Kondisi transformasi dirangkum dalam tabel di bawah berdasarkan nilai dan kontribusi gradien.


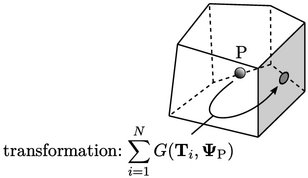
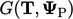 transformasi geometri variabel
transformasi geometri variabel 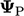 dengan tensor
dengan tensor 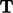 .
.