4.13 Axisymmetric (wedge) Condition

4.13 axisymmetric (wedge) condition

Axisymmetric (wedge) condition. Ada beberapa permasalahan aliran fluida yang geometrinya bersifat aksisimetris. Dengan asumsi solusi aliran adalah axisymmetric, yaitu bidang tidak berubah dalam arah melingkar, mesh komputasi dapat dibentuk dari irisan geometri aliran berbentuk baji.

Jenis mesh untuk solusi axi-simetris ini berisi satu sel melintasi arah melingkar, yang mengurangi jumlah sel menjadi dua dimensi dalam arah aksial dan radial.

Pendekatan terhadap solusi axi-simetris ini menimbulkan kesalahan geometrik karena permukaan-permukaan yang tegak lurus terhadap arah radial menjadi datar. Kesalahan ini berkurang dengan berkurangnya sudut baji; dalam praktiknya, kesalahan dapat dianggap dapat diabaikan untuk sudut 1 $persamaan$ .

Kondisi batas baji diterapkan pada dua bidang miring. Ini mengubah nilai sel 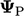$persamaan$ ke permukaan patch menggunakan tensor transformasi 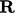$persamaan$ rotasi

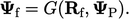f = G(Rf; P): \relax \special {t4ht=

(4.20)

$persamaan$ mendefinisikan rotasiantara vektor satuan $persamaan$ dalam arah melingkar di pusat sel dan vektor satuan menghadap vektor normal $persamaan$ sebesar $persamaan$

Kondisi baji menggunakan kerangka transformasi umum dari Sec. 4.11, dengan nilai eksplisit 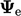$persamaan$ dihitung menggunakan arus 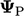$persamaan$ dari Persamaan. (4.20). Gradien eksplisit 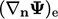$persamaan$ adalah gradien batas 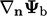$persamaan$ yang dihitung dari 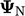$persamaan$ sel tetangga imajiner dengan

C--- rn b = 2 [G(RN; P) P]; \relax \special {t4ht=

(4.21)

tempat perputaran antar pusat sel 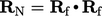$persamaan$ .

Faktor ini 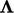$persamaan$ dipilih untuk meminimalkan koefisien batas gradien (lihat Bagian. 4.11). Faktor vektor adalah 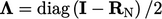$persamaan$ dimana “ 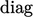$persamaan$ ” didefinisikan dalam Sec. 4.12.

Untuk tensor 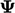$persamaan$ , faktornya adalah 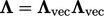$persamaan$ , dengan 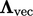$persamaan$ koefisien vektor, seperti yang dijelaskan untuk kondisi simetri pada Sec. 4.12.

Tensor rotasi

Tensor rotasi 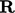$persamaan$ antara dua vektor satuan 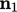$persam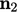aan$ dan $persamaan$ dapat dihitung menggunakan rumus rotasi Euler-Rodrigues,⁶

dimana 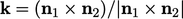$persam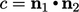aan$ dan $persamaan$ .