Rasio aspek
Bagian sebelumnya menyebutkan sel-sel jaring yang lebih panjang pada satu arah dibandingkan yang lain. Parameter yang digunakan untuk menggambarkan fenomena ini adalah rasio aspek , yang didefinisikan sebagai rasio dimensi terpanjang dan terpendek, 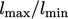 , dari sebuah sel.
, dari sebuah sel.
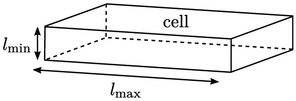
Jaring mencakup sel dengan rasio aspek tinggi untuk efisiensi, dengan memanfaatkan pemahaman sebelumnya bahwa gradien pada beberapa sifat aliran misalnya tegangan geser, laju deformasi dan kecepatan, jauh lebih besar pada satu arah dibandingkan arah lainnya.
Mereka paling sering digunakan untuk menyelesaikan lapisan batas di dinding. Resolusi mesh yang lebih besar diperlukan pada posisi normal pada dinding, dimana gradiennya sangat tinggi, dibandingkan tangensial pada dinding. Ketinggian tengah sel yang berdekatan dengan batas harus sangat kecil, sesuai dengan 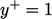 .
.
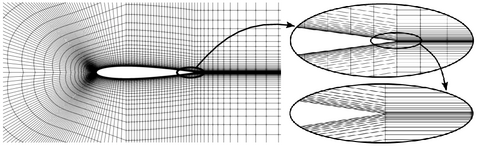
Pada aerofoil di atas, aspek rasionya adalah 1000 di tepi belakang. Jika sel tersebut diganti dengan sel yang memiliki rasio aspek 1, dengan tinggi sel yang sama, jumlah sel akan bertambah 1000 kali lipat, yang menggambarkan besarnya peningkatan efisiensi.
Namun, penerapan rasio aspek yang tinggi di satu area mesh akan menimbulkan masalah di area lain. Contoh aerofoil mempertahankan rasio aspek yang tinggi di luar tepi belakang, dan sebenarnya meningkat hingga 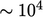 lebih jauh ke hilir. Jika aliran menyimpang dari arah yang sejajar dengan sisi panjang sel dengan rasio aspek tinggi, maka simulasi transien memerlukan aliran yang sangat kecil
lebih jauh ke hilir. Jika aliran menyimpang dari arah yang sejajar dengan sisi panjang sel dengan rasio aspek tinggi, maka simulasi transien memerlukan aliran yang sangat kecil 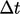 agar berada dalam
agar berada dalam 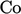 batas wajar. Mesh dapat dimodifikasi dengan secara tiba-tiba mengurangi rasio aspek di luar trailing edge, namun hal ini meningkatkan kesalahan yang terkait dengan diskritisasi.
batas wajar. Mesh dapat dimodifikasi dengan secara tiba-tiba mengurangi rasio aspek di luar trailing edge, namun hal ini meningkatkan kesalahan yang terkait dengan diskritisasi.
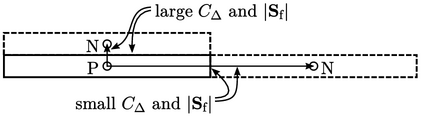
Dengan diskritisasi Laplacian oleh Persamaan. (3.2) dan Persamaan. (3.5), koefisien matriks menyertakan faktor 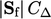 . Pada mesh biasa, keduanya
. Pada mesh biasa, keduanya 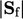 dan
dan  lebih besar untuk permukaan pada sisi terpanjang sel dengan rasio aspek tinggi, dibandingkan sisi terpendek, dengan faktor yang sama dengan rasio aspek. Koefisien matriks dapat berbeda sebesar faktor
lebih besar untuk permukaan pada sisi terpanjang sel dengan rasio aspek tinggi, dibandingkan sisi terpendek, dengan faktor yang sama dengan rasio aspek. Koefisien matriks dapat berbeda sebesar faktor 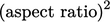 .
.
Konvergensi persamaan tekanan, yang didominasi oleh turunan Laplacian, terkena dampak buruk, khususnya dengan pemecah matriks berbasis CG. Pemecah GAMG bekerja jauh lebih baik karena strategi aglomerasi didasarkan pada pengurangan rasio aspek secara progresif seperti yang dibahas di Bagian. 5.18.
Matriks dengan rentang nilai koefisien yang luas menghasilkan nilai sisa yang lebih rendah  , dihitung dari Persamaan. (5.11). Dengan kata lain, untuk kondisi tertentu
, dihitung dari Persamaan. (5.11). Dengan kata lain, untuk kondisi tertentu  , solusi dengan sel rasio aspek tinggi kurang konvergen dibandingkan solusi tanpa sel. Oleh karena itu, untuk mempertahankan tingkat konvergensi yang setara dengan sel dengan rasio aspek tinggi, kontrol toleransi perlu dikurangi, seringkali beberapa kali lipat.
, solusi dengan sel rasio aspek tinggi kurang konvergen dibandingkan solusi tanpa sel. Oleh karena itu, untuk mempertahankan tingkat konvergensi yang setara dengan sel dengan rasio aspek tinggi, kontrol toleransi perlu dikurangi, seringkali beberapa kali lipat.
