Struktur matriks

Seperti yang dijelaskan dalam Bagian. 3.4, persamaan matriks untuk variabel solusi 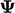berisi sekumpulan koefisien 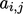yang setiap barisnya 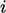sesuai dengan persamaan linier untuk sel dengan indeks 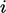sebagai berikut:

$2 3 2 3 2 3 a1;1 a1;2 a1;3 a1;N 1 b1 66 77 66 77 66 77 66 a2;1 a2;2 a2;3 a2;N 77 66 2 77 66 b2 77 66 a3;1 a3;2 a3;3 a3;N 77 66 3 77 = 66 b3 77 66 : : : : : 77 66 : 77 66 : 77 64 :: :: :: :: :: 75 64 :: 75 64 :: 75 aN;1 aN;2 aN;3 aN;N N bN \relax \special {t4ht=$

(5.1)

Ketersebaran matriks

Bayangkan membuat persamaan matriks untuk persamaan transpor untuk medan skalar, misalnya Persamaan. (2.65) dengan sumber panas nol .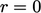

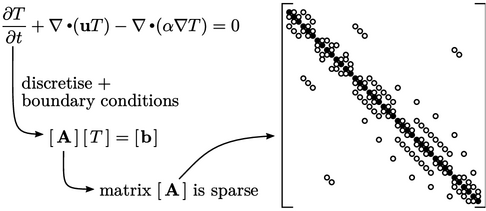
$GAMBAR\santai \khusus {t4ht=$

Gambar tersebut menunjukkan matriks berukuran 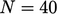, di mana 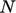adalah jumlah sel. Lingkaran menunjukkan koefisien bukan nol, yang mengisi koefisien diagonal ( 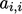). Matriksnya 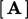sparse yaitu mayoritas koefisiennya adalah 0 (nol ) .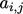

Ketersebaran ini disebabkan oleh setiap sel hanya berinteraksi dengan sel-sel tetangga yang terhubung melalui permukaannya. Misalnya saja 3Djaring sel heksahedral menghasilkan hingga 7 koefisien per baris matriks, dengan satu koefisien diagonal untuk sel tertentu dan 6 koefisien off-diagonal untuk sel tetangga.

Matriks (a)simetri

Matriks simetris mempunyai koefisien yang sama pada diagonalnya, yaitu 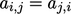. Diskritisasi istilah Laplacian, misalnya 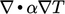, dijelaskan dalam Bagian. 3.7, menghasilkan koefisien yang simetris karena gradien normal permukaan Persamaan. (3.5) menggunakan nilai sel saat ini dan sel tetangga dalam ukuran yang sama.

$GAMBAR\santai \khusus {t4ht=$

Namun, diskritisasi suku adveksi , misalnya 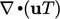, umumnya menghasilkan koefisien asimetris . Misalnya, jika skema melawan arah angin diterapkan untuk aliran dari sel 1 ke sel 2, maka akan ada kontribusi terhadap 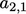tetapi tidak terhadap .

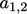Ukuran matriks

Simulasi paralel memungkinkan solusi yang terjangkau pada jerat yang besar. Untuk ukuran mesh 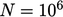, matriksnya akan mempunyai 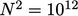koefisien, 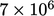yang biasanya tidak nol.

Untuk alasan efisiensi, koefisien nol tidak disimpan dalam memori komputer. Sebaliknya, penyimpanan menyediakan array dengan koefisien bukan nol dan array pengalamatan dari indeks baris dan kolom yang sesuai untuk setiap koefisien.