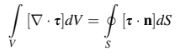2.5.4 Teorema Divergensi
Biarkan V mewakili suatu volume dalam ruang tiga dimensi (Gambar 2.17) dengan batas S. Biarkan n menjadi vektor satuan yang mengarah ke luar dari S. Jika v adalah suatu medan vektor yang didefinisikan pada V, maka teorema divergensi [30, 31] (juga dikenal sebagai teorema Gauss) menyatakan bahwa,
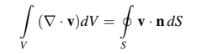
Teorema divergensi menyiratkan bahwa fluks bersih dari suatu medan vektor melalui suatu permukaan tertutup sama dengan volume total dari semua sumber dan lubang (yaitu, integral volume dari divergensinya) di dalam wilayah di dalam permukaan tersebut. Ini merupakan teorema penting dalam dinamika fluida.
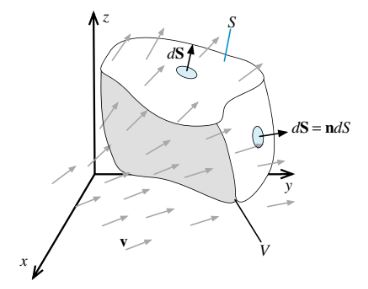
Gambar 2.17 Sebuah volume dalam ruang tiga dimensi dengan batas yang terdiri dari potongan-potongan yang halus secara piecewise (S).
Teorema divergensi dapat digunakan dalam berbagai konteks untuk mendapatkan banyak identitas (korolari) lain yang berguna [32]. Secara khusus, teorema ini dapat diterapkan pada hasil kali antara suatu fungsi skalar s dan suatu vektor konstan yang bukan nol untuk mendapatkan hubungan penting berikut:
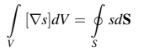
Teorema divergensi sama-sama dapat diterapkan pada tensor, dalam hal ini dituliskan sebagai,