2.5.5 Aturan Integral Leibniz
Aturan integral Leibniz memberikan formula untuk menghitung turunan integral tentu yang batasnya merupakan fungsi dari variabel diferensial [33–36]. Biarkanmenjadi suatu fungsi yang bergantung pada variabel ruang x dan waktu t. Maka aturan integral Leibniz dapat dinyatakan sebagai berikut:
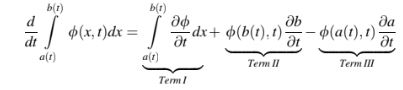
Makna berbagai istilah dalam Persamaan (2.87) dapat ditarik kesimpulannya dari Gambar 2.18. Istilah pertama di sisi kanan memberikan perubahan dalam integral karenaberubah dengan waktu t, sementara istilah kedua dan ketiga memperhitungkan penambahan dan pengurangan luas saat batas atas dan bawah dipindahkan, masing-masing.
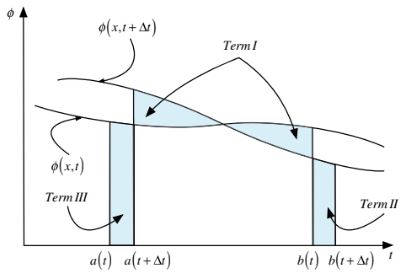
Gambar 2.18 Kurva yang menunjukkan distribusi spasial suatu fungsi pada waktu t dan
Bentuk tiga dimensi dari rumus ini yang diterapkan pada suatu volume V(t) yang dibatasi oleh suatu permukaan S(t) dengan elemen permukaannya bergerak dengan kecepatandapat dituliskan sebagai berikut:
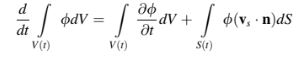
di manaadalah suatu fungsi skalar dari ruang dan waktu. Untuk suatu volume V yang tidak bergerak, persamaannya dapat disederhanakan menjadi:
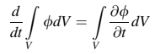
Persamaan-persamaan di atas juga dapat diterapkan pada vektor dan tensor.
