6.4.1 informasi topologi (koneksi)
Informasi topologi (koneksi). Seperti yang ditunjukkan pada Gambar 6.9, informasi topologi dikembangkan dengan secara eksplisit membangun indeks lokal, Gambar 6.9a, dan global, Gambar 6.9b, yang mendefinisikan konektivitas komponen geometris (elemen ke elemen, elemen ke wajah, wajah ke elemen, elemen ke node, dll.). Untuk tujuan ini, struktur data dari elemen, wajah, dan node sekarang mencakup informasi tentang konektivitas tetangga dalam hal indeks lokal dan global.
Algoritma perhitungan gradien sekarang dapat diungkapkan dalam hal indeks diskritisasi yang ditunjukkan pada Gambar 6.9a sebagai berikut,

atau dalam hal nomor lokal wajah elemen yang ditunjukkan pada Gambar 6.9a sebagai berikut,
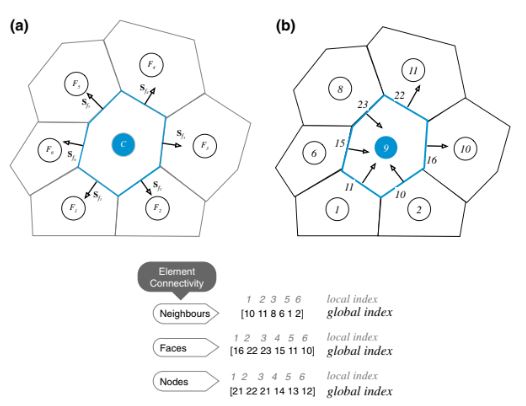
Gambar 6.9 Koneksi elemen dan orientasi wajah menggunakan a indeks lokal dan b indeks global
di mana tanda “()” menunjukkan indeks lokal dari wajah. Hubungan gradien juga dapat ditulis dalam hal indeks global yang mewakili nilai yang disimpan di wajah elemen seperti yang ditunjukkan pada Gambar 6.9b sebagai berikut,
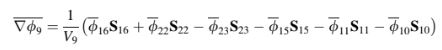
di mana perlu dicatat bahwa tanda negatif untuk istilah-istilah wajah 23, 15, 11, dan 10. Sementara vektor permukaan lokal S selalu diasumsikan mengarah ke luar, ini tidak selalu benar, karena hanya satu vektor normal yang disimpan di setiap wajah. Dengan melihat Gambar 6.9, vektor permukaan yang disimpan khusus ini sebenarnya mengarah ke dalam elemen 9, oleh karena itu tanda negatif. Berbeda dengan sistem grid terstruktur di mana arah yang benar dapat dengan mudah diperoleh, dalam grid tak terstruktur arah normal ke permukaan harus disimpan dengan cara tertentu. Ini akan dijelaskan secara rinci dalam bagian berikutnya. Untuk memperhitungkan arah vektor, fungsi tanda digunakan dan persamaan untuk gradien dimodifikasi sebagai berikut,
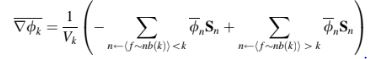
Untuk wajah, informasi tentang elemen-elemen yang saling berdampingan adalah yang mendefinisikan topologi wajah. Selain itu, orientasi wajah dapat didefinisikan dengan cara standar dengan memberikan indeks pada elemen-elemen dalam urutan tertentu. Dalam hal ini, vektor normal pada antarmuka antara dua elemen diarahkan dari elemen 1 ke elemen 2, yang juga dinotasikan di OpenFOAM® sebagai elemen pemilik dan tetangga, masing-masing, seperti yang ditunjukkan pada Gambar 6.10.
Oleh karena itu, jika antarmuka dianggap dengan elemen 2, maka harus dikalikan dengan tanda negatif. Dengan demikian, mempertimbangkan wajah yang membatasi elemen 9, informasi konektivitas didefinisikan seperti yang ditunjukkan dalam Gambar 6.11.
Perhitungan gradien dapat dilakukan untuk setiap elemen. Namun, karenapada setiap antarmuka sama untuk elemen yang saling berdampingan dengan elemen,
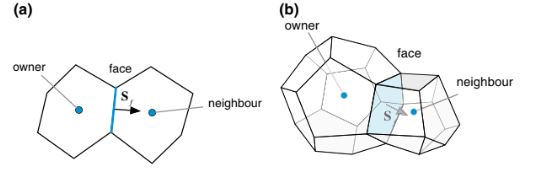
Gambar 6.10 Pemilik, tetangga, dan wajah untuk a elemen 2D dan b elemen 3D
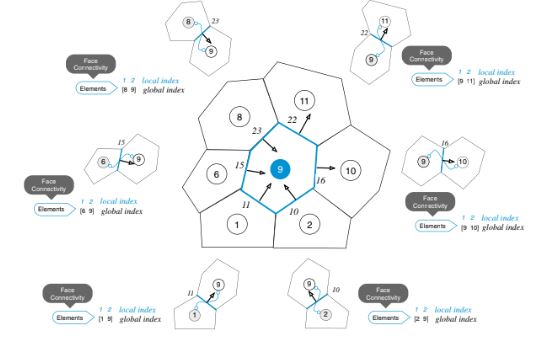
Gambar 6.11 Contoh konektivitas wajah, elemen, dan node untuk grid tak terstruktur
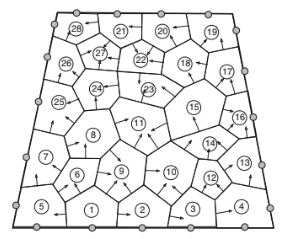
Gambar 6.12 Sistem Mesh Tanpa Struktur
perbedaan pada tanda, perhitungan gradien dapat dilakukan dengan cara yang lebih efisien dengan menghitung gradien di seluruh domain (misalnya, seluruh domain yang ditunjukkan dalam Gambar 6.12) daripada elemen demi elemen. Ini dilakukan dengan melintasi semua wajah (faces) dalam domain perhitungan dan langsung memperbarui nilai gradien untuk elemen yang melintasi antarmuka dengan menambah dan mengurangkan fluks yang dihitung dari gradien elemen 1 dan elemen 2, secara berturut-turut. Oleh karena itu, algoritma pada grid tanpa struktur untuk menghitung lapangan gradien menjadi
Algoritma untuk menghitung gradien pada sistem grid tanpa struktur:

Ini pada dasarnya menghasilkan gradien di setiap elemen dalam domain perhitungan sesuai dengan Persamaan (6.20). Algoritma yang sama dapat digunakan dengan grid terstruktur untuk mengurangi biaya komputasinya.
