6.5.2.3 Faktor Pembobotan Wajah
Faktor pembobotan wajah. Pertimbangkan sistem mesh volume hingga satu dimensi yang ditunjukkan dalam Gambar 6.22. Nilai-nilai dari φ diketahui di pusat massa sel kontrol C dan F, dan akan digunakan untuk menghitung nilai φ di antarmuka f.
Interpolasi linear sederhana akan menghasilkan rumus berikut:
dimana
Kesederhanaan rumus ini tidak berlanjut ke dalam situasi multi-dimensi seperti dalam dua atau tiga dimensi, di mana keadaannya menjadi sedikit lebih rumit. Dalam hal ini, tidak ada opsi tunggal untuk definisi faktor pembobotan geometris.
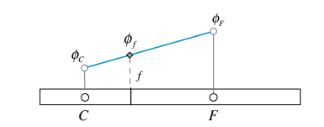
Gambar 6.22 Sistem mesh satu dimensi
Salah satu pilihan adalah untuk membangun faktor pembobot berdasarkan pada volume masing-masing, sehingga
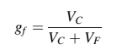
Namun, ini menghasilkan hasil yang salah dalam beberapa kasus, seperti pada konfigurasi yang ditunjukkan pada Gambar 6.23. Kesulitan lain muncul ketika titik C, f, dan F tidak sejajar seperti yang digambarkan pada Gambar 6.24a. Alternatif yang lebih baik untuk kasus-kasus seperti ini, seperti yang ditampilkan pada Gambar 6.24b, adalah membangun interpolasi berdasarkan jarak normal ke permukaan, yaitu, Cf’ dan Ff”. Dengan demikian, faktor interpolasi dihitung sebagai
di manaadalah vektor satuan permukaan yang diberikan oleh,
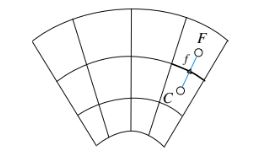
Gambar 6.23 Sistem grid aksisimetris
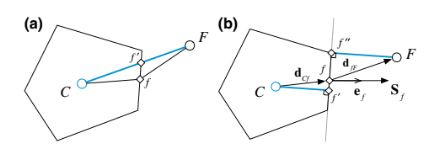
Gambar 6.24 Volume kendali dua dimensi dengan titik C, f, dan F yang tidak sejajar.
