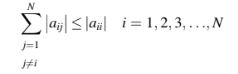10.3.1 Metode Jacobi
Mungkin yang paling sederhana dari metode iteratif untuk menyelesaikan sistem persamaan linear adalah metode Jacobi, yang disajikan secara grafis dalam Gambar 10.2.
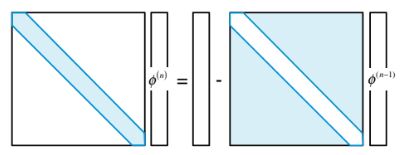
Gambar 10.2 Representasi grafis dari metode Jacobi
Mempertimbangkan sistem persamaan yang dijelaskan oleh Persamaan (10.1), jika elemen diagonal tidak nol, maka persamaan pertama dapat digunakan untuk memecahkan , persamaan kedua untuk memecahkan
dan seterusnya. Proses solusi dimulai dengan memberikan nilai tebakan untuk vektor tak diketahui
Nilai tebakan ini digunakan untuk menghitung perkiraan baru dimulai dengan
, kemudian
dan perhitungan dilanjutkan hingga perkiraan baru untuk
dihitung. Ini merupakan satu iterasi. Hasil yang diperoleh diperlakukan sebagai tebakan baru untuk iterasi berikutnya dan proses solusi diulang. Iterasi berlanjut hingga perubahan dalam prediksi antara dua iterasi berurutan turun di bawah nilai yang hampir nol atau hingga suatu kriteria konvergensi yang telah ditetapkan terpenuhi. Begitu ini terjadi, solusi final tercapai. Dalam metode ini, dengan memberikan suatu estimasi saat ini
pembaruan diperoleh menggunakan hubungan berikut:
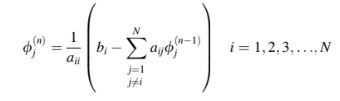
Persamaan (10.71) menunjukkan bahwa nilai yang diperoleh selama suatu iterasi tidak digunakan dalam perhitungan selama iterasi yang sama, melainkan disimpan untuk iterasi berikutnya. Dengan menggunakan matriks, bentuk ekspansi dari Persamaan (10.71) diberikan oleh

Memecahkan untuk , Persamaan (10.72) memberikan

Dengan menggunakan Persamaan (10.46) dan (10.73), dapat dituliskan lebih ringkas sebagai
Metode Jacobi akan konvergen selama Kondisi ini dipenuhi untuk kelas matriks yang besar termasuk yang dominan diagonal di mana koefisiennya memenuhi