10.3.3 Prekondisioning dan Metode Iteratif

Laju konvergensi dari metode iteratif tergantung pada sifat spektral matriks iterasi B, yang tergantung pada matriks koefisien. Berdasarkan itu, metode iteratif mencari transformasi dari sistem persamaan menjadi yang setara dengan solusi yang sama, tetapi dengan sifat spektral yang lebih baik. Dalam kondisi ini, nilai eigen dari sistem yang setara lebih terkumpul, memungkinkan solusi iteratif untuk diperoleh lebih cepat daripada dengan sistem asli. Prekondisi didefinisikan sebagai matriks yang mempengaruhi transformasi tersebut. Matriks prekondisi P didefinisikan sedemikian rupa sehingga sistem

Memiliki solusi yang sama dengan sistem asli tetapi propertis spektral dari matriks koefisiennya lebih kondusif. Dalam mendefinisikan prekondisioner P, kesulitannya adalah menemukan matriks yang mendekati dan mudah diinvers (yaitu, untuk menemukan ) dengan biaya yang wajar. Menuliskan kembali Pers. (10.47), namun sekarang dengan P menggantikan M (yaitu, M = P dan A = P – N) sistem iterasi titik tetap terkait diberikan oleh

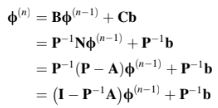
yang dalam bentuk residu dapat ditulis sebagai

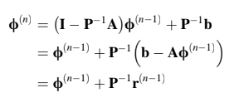
Dari kedua persamaan tersebut, sekarang jelas bahwa prosedur iteratif hanyalah iterasi titik tetap pada sistem yang diprekonisi yang terkait dengan dekomposisi A = P – N di mana propertis spektralnya sekarang

Dengan membandingkan, matriks prekondisioning untuk metode Jacobi (J) dan Gauss-Seidel (GS) adalah hanya

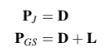
Di mana D dan L masing-masing merupakan bagian diagonal dan segitiga bawah dari matriks A. Dengan demikian, prekondisioning adalah manipulasi dari sistem asli untuk meningkatkan propertis spektralnya dengan matriks prekondisioning P yang digunakan dalam prosedur iteratif terkait. Seperti yang akan dijelaskan dalam bagian-bagian berikutnya, adalah mungkin untuk mengembangkan matriks prekondisioning yang lebih canggih di mana koefisien-koefisiennya didefinisikan dengan cara yang lebih kompleks.