12.1 Formulasi Variabel Terormalisasi (NVF)
Formulasi Variabel Terormalisasi (NVF) adalah kerangka kerja untuk deskripsi dan analisis skema Resolusi Tinggi (HR). Ini diperkenalkan oleh Leonard [1–3] dan populer dengan Kriteria Batasan Konveksi (CBC) yang disederhanakan oleh Gaskell dan Lau [4]. Diagram Variabel Terormalisasi (NVD) adalah alat yang berguna untuk pengembangan dan analisis skema HO dan HR. NVF adalah prosedur formulasi wajah yang didasarkan pada normalisasi lokal variabel tergantung untuk nilaipada wajah f yang akan dibangun. Pendekatan ini bergantung pada nilai simpul upwind (
) downwind (
)dan far upwind (
) seperti yang ditunjukkan dalam Gambar 12.1, untuk mengekspresikan variabel yang dinormalisasi sebagai
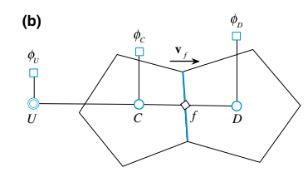
Gambar 12.1 adalah skema yang menunjukkan lokasi simpul U, C, dan D yang digunakan dalam menjelaskan skema konveksi pada grid terstruktur b simpul C, D, dan simpul U yang diekstrapolasi untuk grid tak terstruktur.

Dengan normalisasi ini, hubungannya
diubah menjadi
karena nilai yang dinormalisasi daridan
menjadi sama dengan
sedangkan nilai yang dinormalisasi dari menjadi indikator kelancaran untuk bidang
. Nilai-nilai
antara 0 dan 1
menggambarkan profil monotomik, sedangkan nilai-nilai
yang kurang dari 0
atau lebih besar dari 1
menunjukkan ekstremum pada C. Selain itu, nilai-nilai
yang sama dengan 0 atau 1 menunjukkan loncatan gradien. Konfigurasi-konfigurasi ini diilustrasikan dalam Gambar 12.2. Normalisasi juga berguna untuk mengubah hubungan fungsional dari skema HO menjadi hubungan linear antara
dan
Sebagai contoh, hubungan fungsional yang dinormalisasi dari skema HO yang disajikan dalam bab sebelumnya adalah sebagai berikut:
Upwind:
Differensi Tengah:
Upwind Orde Kedua:
FROMM:
QUICK:
Downwind:
Dengan demikian, untuk semua skema HO yang didasarkan pada tiga nilai simpul, selalu dapat diekspresikan sebagai fungsi linear dari
di mana nilai dari L dan k tergantung pada skema tersebut. Oleh karena itu, jika
digambarkan sebagai fungsi dari
dalam bidang
maka hubungan fungsional dari skema-skema ini akan muncul sebagai garis lurus pada plot. Plot hasilnya ditandai dengan Diagram Variabel Terormalisasi (NVD). Sebuah NVD di mana hubungan fungsional dari skema-skema di atas digambarkan ditampilkan dalam Gambar 12.3.
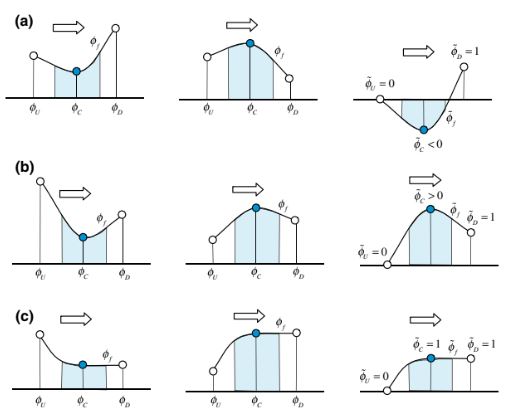

Gambar 12.2 Skema situasi ketika a dan e
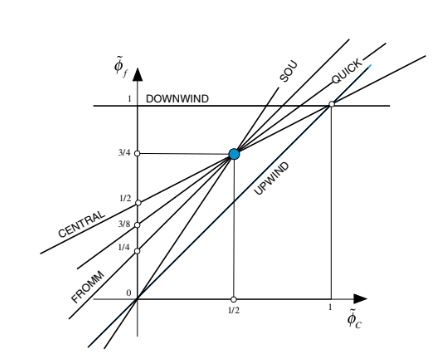
Gambar 12.3 Beberapa skema HO yang ditulis dalam bentuk terormalisasi dan diplot pada Diagram Variabel Terormalisasi (NVD).
Skema HO yang disajikan dalam bab sebelumnya telah terbukti secara drastis mengurangi kesalahan pemangkasan yang dialami oleh skema hulur pertama ke atas, sementara tetap stabil. Namun, salah satu kekurangan utama dari skema-skema ini adalah ketidakterbatasan mereka, yaitu, kecenderungan mereka untuk menghasilkan lonjakan dan/atau osilasi bahkan dekat dengan lonjakan tiba-tiba atau gradien curam dalam variabel terkonveksi (lihat Gambar 11.14b dan 11.17). Meskipun dalam beberapa aplikasi, lonjakan kecil dan/atau osilasi mungkin dapat ditoleransi, dalam yang lain, mereka dapat menyebabkan hasil yang katastropik, seperti dalam perhitungan aliran turbulen di mana variabel terkonveksi dapat menjadi koefisien viskositas.
Perilaku osilasi dekat dengan gradien curam ini mencirikan semua skema konvektif linear HO. Faktanya, skema-skema ini tidak monoton dalam arti bahwa mereka menghasilkan maksima lokal dan/atau minima, yaitu, mereka tidak mempertahankan ekstremum. Agar sebuah skema mempertahankan ekstremum, maksima dalam solusi harus tidak meningkat dan minima tidak menurun (skema tidak boleh menghasilkan lonjakan atas/bawah). Faktanya, telah didemonstrasikan oleh Godunov dan Ryabenki [5] bahwa setiap skema numerik linear yang monotone paling banyak dapat akurat orde pertama. Ini menyiratkan bahwa semua skema linear orde tinggi tidak dapat mempertahankan monotonisitas, dan bahwa untuk membuat skema yang mempertahankan monotonisitas, fungsi pembatas non-linear harus digunakan. Dengan pemahaman ini, kerja pengembangan skema konvektif bebas osilasi orde tinggi menghasilkan beberapa teknik [6–10] yang dapat dikelompokkan dalam dua kategori. Pada pendekatan pertama [11–13], aliran antidi-fusif yang terbatas ditambahkan ke skema hulur pertama ke atas dengan cara sehingga skema yang dihasilkan mampu memecahkan gradien tajam tanpa osilasi. Pada kategori kedua, aliran difusif penyamaran diperkenalkan ke dalam skema HO yang tidak terbatas untuk meredam osilasi tidak fisik [14–17].
Karena sifat multi-langkah mereka dan kesulitan dalam menyeimbangkan dua aliran, teknik penggabungan aliran cenderung sangat mahal secara numerik. Oleh karena itu, dalam buku ini dua pendekatan untuk pengembangan skema HR yang masuk dalam metode pembatas aliran akan disajikan. Pendekatan pertama mengikuti prosedur gabungan di mana skema orde tinggi digabungkan dengan yang rendah, dengan perpindahan antara keduanya dikendalikan oleh suatu kriteria tertentu [18]. Metode kedua didasarkan pada penambahan ke sebuah term hulur pertama ke atas yang difusif aliran anti-difusif yang dikalikan dengan pembatas aliran. Dalam kasus ini, skema HR yang dihasilkan juga ditunjukkan dengan skema Penurunan Variasi Total (TVD) seperti yang dijelaskan dalam bagian selanjutnya.
Pendekatan skema gabungan akan disajikan pertama kali dalam kerangka Kerangka Variabel Terormalisasi (NVF) dan akan divisualisasikan pada Diagram Variabel Terormalisasi (NVD). Oleh karena itu, NVF dan NVD pertama-tama dijelaskan. Penggunaan NVD akan menjadi kunci untuk definisi suatu kriteria yang memastikan keterbatasan dari setiap skema interpolasi orde tinggi.
