12.2 Kriteria Batasan Konveksi (CBC)

Kriteria batasan konveksi (CBC). Sebuah skema numerik diharapkan dapat mempertahankan sifat-sifat fisik dari fenomena yang sedang mencoba untuk dijelaskan atau diaproksimasi. Oleh karena itu, kondisi yang harus dipenuhi oleh suatu skema konveksi yang terbatas dapat dipahami dengan baik dengan menganalisis sifat-sifat fisik dari konveksi. Karena konveksi mengangkut sifat-sifat fluida dari hulu ke hilir, maka aproksimasi terhadap konveksi harus memiliki atribut transportasi ini. Oleh karena itu, skema konveksi numerik harus cenderung ke hulu (upwind biased) atau jika tidak mereka akan kehilangan stabilitas konvektif. Oleh karena itu, selain dari nilai pada simpul-simpul yang merentang antarmuka dannilai pada simpul yang jauh ke hulu, yaitu juga penting dalam menganalisis skema advective. Nilai-nilai pada simpul-simpul yang lebih jauh kurang penting. Dalam NVF yang disajikan di atas, nilai-nilai dinormalisasi sedemikian rupa sehingga efek dari juga dipertimbangkan. Ini sangat berguna karena membantu mengidentifikasi kondisi di mana skema konveksi numerik adalah monoton. Sedangkan definisi skema monotone (atau skema terbatas) dari Spekreise [19] dan Barth dan Jespersen [20] melibatkan semua tetangga yang mengelilingi wajah, Leonard [21] dan Gaskel dan Lau [4] berdasarkan definisi mereka tentang monoton hanya pada titik-titik tetangga sepanjang sistem koordinat lokal sehingga

Dengan melakukan normalisasi, kondisi di atas menjadi

Kriteria Batasan Konveksi (CBC) untuk perhitungan aliran steady state implisit yang dikembangkan oleh Gaskell dan Lau menyatakan bahwa untuk sebuah skema memiliki sifat terbatas, hubungan fungsionalnya harus kontinu, harus terbatas dari bawah oleh dan dari atas oleh satu, dan harus melewati titik-titik (0, 0) dan (1, 1), dalam rentang monotonic dan untuk atauhubungan fungsional harus sama dengan Kondisi di atas diilustrasikan pada NVD dalam Gambar 12.4, dapat dirumuskan secara matematis sebagai

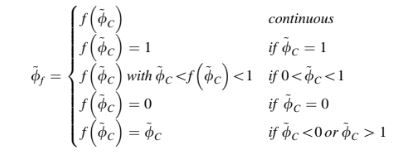
Kriteria Batasan Konveksi cukup intuitif dan dapat diinterpretasikan dengan merujuk pada Gambar 12.4 dan 12.5. Ketika berada dalam profil monotomik, profil interpolasi di permukaan sel tidak boleh menghasilkan ekstremum baru. Oleh karena itu, hal ini dibatasi oleh nilai-nilaipada simpul-simpul yang merentang wajah. Ketika nilai mendekati sementara masih dalam rezim monotomik, nilaijuga akan cenderung menuju . Ketika menjadi sama dengan makajuga menjadi sama dengan

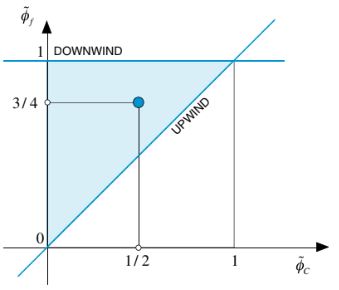
Gambar 12.4 Kriteria Batasan Konveksi (CBC) pada Diagram NVD yang menunjukkan wilayah di manadibatasi.

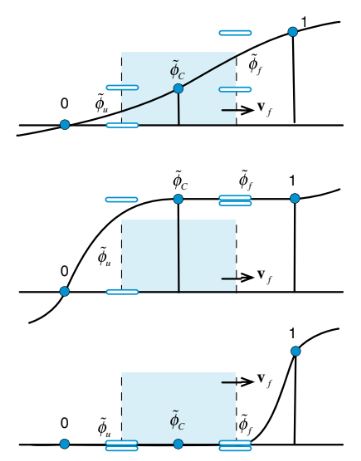
Gambar 12.5 Nilai dan Kriteria Batasan Konveksi.

oleh karena itu, kondisi bahwa melewati titik (1, 1). Ketika nilai adalah diberikan nilai hulu, yaitu, Ini memiliki efek menghasilkan kondisi aliran keluar terbesar yang mungkin sambil memenuhi kondisi bahwa dibatasi oleh simpul-simpul yang merentang wajah sel. Perilaku ini berarti bahwa setiap osilasi yang tidak pantas akan meredup karena akan cenderung menuju nilai yang lebih rendah karena aliran keluar lebih besar dari pada aliran masuk dalam kondisi-kondisi ini.

Oleh karena itu jika tidak ada mekanisme fisik eksternal yang menghasilkan ekstrema (misalnya, sebuah istilah sumber) maka ekstrema akan padam. Mekanisme serupa terjadi ketika Namun ketika semakin mendekati yang berasal dari daerah non-monotonik, akan sama dengan nilai hulu sampai menyiratkan kondisi bahwa profil melewati titik (0, 0). Ketika solusi akan berada di wilayah di mana konveksi dominan dan pendekatan hulu akan menjadi sangat baik.