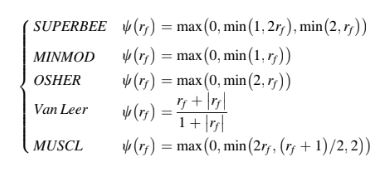12.4 Kerangka Kerja TVD
Kerangka kerja TVD. Pendekatan lain yang populer untuk mengembangkan skema konvektif HR adalah kerangka kerja Total Variation Diminishing (TVD). Dalam menyelesaikan secara numerik sebuah persamaan diferensial parsial adveksi untuk suatu variabel / dalam bentuk yang telah disajikan sejauh ini, Total Variation (TV) didefinisikan sebagai
di mana i mewakili indeks dari simpul dalam domain solusi spasial. Sebuah metode numerik dikatakan Total Variation Diminishing (TVD) jika TV dalam solusi tidak meningkat seiring waktu. Secara matematis, ini setara dengan
Dalam makalahnya yang berpengaruh, Harten [26] membuktikan bahwa skema monoton adalah TVD, dan skema TVD mempertahankan monotonisitas. Sebuah skema yang mempertahankan monotonisitas tidak menciptakan ekstremum lokal baru dalam domain solusi, yaitu, nilai minimum lokal tidak menurun, dan nilai maksimum lokal tidak meningkat. Di sini tidak dimaksudkan untuk memberikan turunan matematis lengkap dari pendekatan TVD. Sebaliknya, tujuannya hanyalah untuk menjelaskan metodologi dalam membangun skema TVD. Pendekatan yang digunakan didasarkan pada karya Sweby [27].
Pertimbangkan persamaan konveksi satu dimensi tak-stasioner (11.73), yang digunakan dalam bab sebelumnya untuk mempelajari stabilitas skema konveksi. Dalam ketiadaan difusi dan sumber, persamaan ini dapat direduksi menjadi
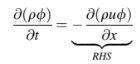
Bentuk diskritisasi umum dari istilah RHS berdasarkan stencil lima titik dapat ditulis sebagai
di mana U, C, dan D mewakili simpul jauh ke hulu, hulu, dan hilir, seperti yang ditunjukkan dalam Gambar 12.1a. Sweby dan Harten membuktikan bahwa kondisi yang cukup bagi sebuah skema numerik yang disajikan oleh Persamaan (12.27) untuk menjadi TVD atau monoton adalah untuk koefisien per laju aliran massa memenuhi ketidaksetaraan
di mana ekspresi untuk koefisien a dan b tergantung pada skema konveksi yang diadopsi. Kembali merujuk pada skema konveksi yang disajikan di atas, ditemukan bahwa skema hulu orde pertama sangat difusif sementara skema perbedaan sentral orde kedua sangat dispersif. Diperlukan suatu skema yang berada di antara skema hulu dan perbedaan sentral, yaitu, skema yang memiliki stabilitas skema hulu dan akurasi skema perbedaan sentral. Skema seperti itu dapat dibangun dengan memulai dari skema perbedaan sentral yang ditulis sebagai
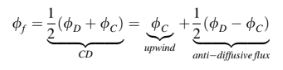
di mana notasi yang digunakan sebelumnya diadopsi dengan C menunjukkan simpul hulu, D simpul hilir, dan f nilai di permukaan sel yang merentang antara simpul C dan D. Seperti yang diimplikasikan oleh Persamaan (12.29), skema perbedaan sentral dapat ditulis sebagai jumlah dari skema hulu dan fluks yang seharusnya bersifat anti-difusif karena skema CD bersifat dispersif. Fluks ini diinginkan karena membuat skema menjadi akurat orde kedua. Efek sampingnya adalah osilasi yang tidak fisik yang diciptakannya karena penurunan difusi numerik. Oleh karena itu, pendekatan yang lebih baik adalah dengan menambahkan sebagian dari fluks anti-difusif ini ke skema hulu sedemikian rupa sehingga akurasi orde kedua tetap terjaga tanpa menciptakan osilasi yang tidak fisik. Salah satu cara untuk melakukannya adalah dengan mengalikan fluks ini dengan fungsi pembatas (juga disebut pembatas atau pembatas fluks) yang akan mencegah penggunaannya yang berlebihan di daerah di mana osilasi mungkin terjadi (misalnya, melintasi gradien besar) sambil memaksimalkan kontribusinya di daerah yang halus. Dengan menunjukkan pembatas semacam itu dengan di mana r biasanya diambil sebagai rasio dari dua gradien berturut-turut,
dihitung sebagai
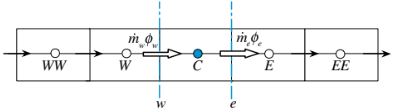
Gambar 12.8 Fluks konvektif dalam domain satu dimensi
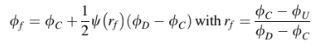
di mana U adalah simpul hulu dari C dan D adalah simpul hilir dari C. Untuk mempertahankan tanda fluks anti-difusif, diambil sebagai nonnegatif. Oleh karena itu, mengembangkan sebuah skema TVD berkurang menjadi menemukan pembatas yang akan membuat skema numerik TVD atau monoton. Kondisi-kondisi yang harus dipenuhi oleh pembatas ini agar skema konveksi dapat mempertahankan monotonitasnya akan diuraikan selanjutnya dengan memanggil pembatas fluks dalam diskritisasi dari RHS Persamaan (12.27) melalui nilai antarmuka yang diberikan oleh Persamaan (12.30). Mempertimbangkan domain satu dimensi yang ditunjukkan dalam Gambar 12.8, fluks konvektif di permukaan elemen diberikan oleh
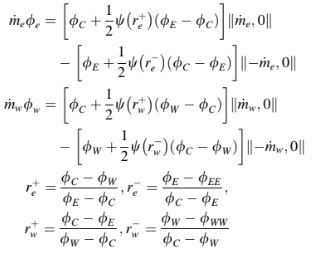
Untuk menyederhanakan turunan yang akan datang, diasumsikan bahwa kecepatan positif. Dalam kondisi-kondisi ini, bentuk diskritisasi dari RHS Persamaan (12.24) diperoleh sebagai
sedangkan persamaan kontinuitas diberikan oleh
Dengan memanggil batasan kontinuitas, persamaan RHS dapat diatur ulang menjadi
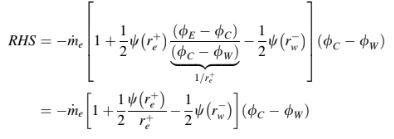
Dengan membandingkan Persamaan (12.34) dengan Persamaan (12.27), nilai-nilai dari a dan b ditemukan sebagai
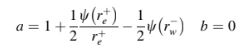
Agar skema menjadi TVD, yang berikut harus berlaku [Persamaan (12.28)]:
yang dapat diperluas menjadi
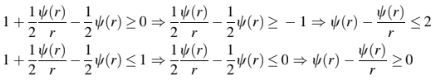
atau dengan kata lain
Jika selain memiliki sebuah kondisi diberlakukan di mana
untuk nilai-nilai negatif dari r, maka kondisi di atas akan dipenuhi jika
Dengan menggabungkan semua kondisi yang harus dipenuhi oleh pembatas untuk menghasilkan skema TVD, sebuah kriteria yang mirip dengan CBC dapat dikembangkan dan diberikan oleh
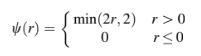
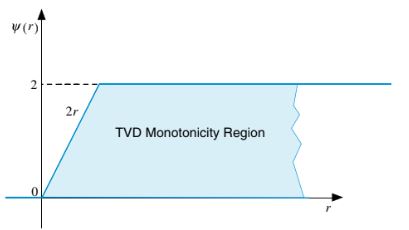
Gambar 12.9 Wilayah monotonisitas TVD pada diagram
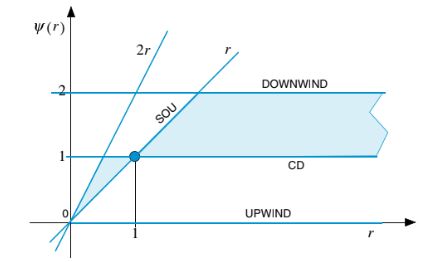
Gambar 12.10 Pembatas skema SOU dan CD pada diagram
Seperti yang digambarkan dalam Gambar 12.9, kondisi-kondisi ini dapat digambarkan pada diagram , yang juga disebut diagram Sweby, untuk menunjukkan wilayah monotonitas TVD (wilayah biru dalam plot). Dengan menggunakan diagram ini, mudah untuk memahami formulasi skema TVD. Setiap pembatas fluks
yang dirumuskan untuk berada dalam wilayah monotonisitas TVD menghasilkan skema TVD. Diagram Sweby sangat mirip dengan NVD yang disajikan di atas.
Pembatas untuk semua skema yang telah disajikan sejauh ini dapat diperoleh dan hubungan fungsional mereka digambarkan pada diagram Sweby. Secara khusus, pembatas CD dengan mudah diperoleh dari Persamaan (12.29) sebagai sedangkan untuk skema SOU dapat dihitung sebagai berikut:
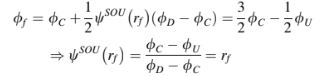
Pembatas untuk kedua skema ditampilkan di Gambar 12.10. Sweby [27] juga mencatat bahwa karena untuk
akurasi orde kedua hilang pada ekstremum dari solusi. Skema SOU dan CD adalah skema orde kedua dan dengan memeriksa Gambar 12.10 jelas terlihat bahwa keduanya melewati titik (1, 1). Selain itu, seperti yang ditunjukkan dalam karya Van Leer [28], setiap skema orde kedua dapat ditulis sebagai rata-rata tertimbang dari skema CD dan SOU. Oleh karena itu, agar sebuah skema menjadi orde kedua, pembatasnya harus melewati titik (1, 1) dan, seperti yang ditunjukkan di Gambar 12.10, pembatasnya harus berada dalam wilayah yang dibatasi oleh pembatas CD dan SOU (wilayah biru dalam plot). Wilayah yang sesuai pada NVD ditunjukkan di Gambar 12.11.
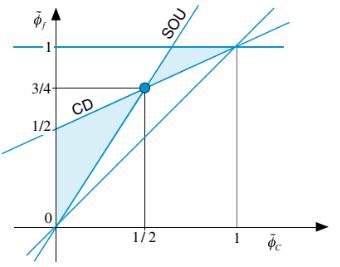
Gambar 12.11 Wilayah pada NVD yang setara dengan wilayah monotonisitas TVD pada diagram Sweby untuk skema orde kedua.
Dengan mengadopsi pendekatan ini dan mengikuti prosedur yang digunakan dengan skema SOU, hubungan fungsional pembatas untuk banyak skema HO yang disajikan di atas dapat dengan mudah dihitung dan diberikan oleh:

Skema FROMM adalah rata-rata dari skema CD dan SOU. Hubungan fungsionalnya secara matematis ditulis sebagai:
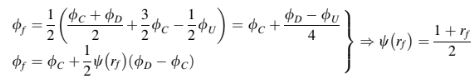
Hubungan fungsional dari pembatas-pembatas ini ditampilkan di Gambar 12.12. Dengan pengecualian pembatas skema upwind, semua pembatas lainnya terlihat tidak sepenuhnya berada dalam wilayah monotonisitas. Dengan demikian, skema-skema ini tidak terbatas.
Dengan membatasi fungsi dari berbagai skema di atas untuk berada dalam wilayah monotonisitas yang ditampilkan di Gambar 12.9, skema-skema HO ini diubah menjadi skema HR TVD. Banyak skema TVD telah dikembangkan dengan cara itu dan pembatas untuk sejumlah dari mereka ditunjukkan di Gambar 12.13a–d dengan hubungan fungsional pembatas mereka diberikan oleh
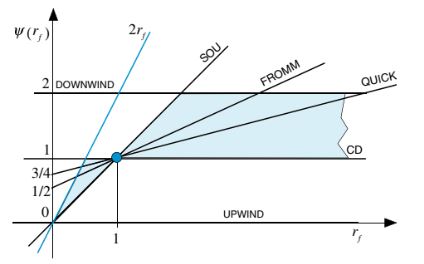
Gambar 12.12 Skema Orde Tinggi dan Wilayah Monotonisitas TVD pada diagram Sweby
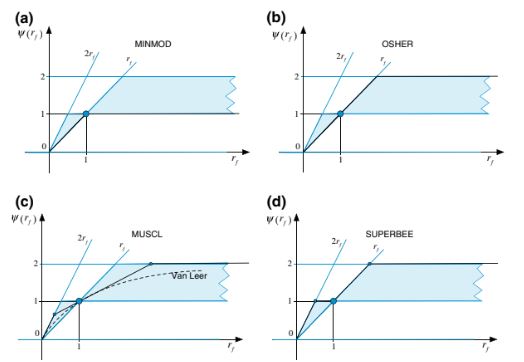
Gambar 12.13 Pembatas dari skema TVD a MINMOD, b OSHER, c MUSCL, dan d SUPERBEE pada diagram Sweby