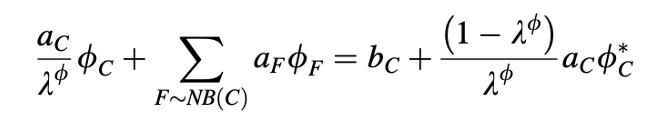infistream

Menu

Patankar’s Under-Relaxation

Seperti yang disebutkan di atas, solusi iteratif dari sistem persamaan dapat direlaksasi bawah dengan memperkenalkan faktor relaksasi πœ†βˆ… dan diungkapkan melalui Persamaan (14.6). Untuk menyederhanakan notasi yang digunakan dengan relaksasi bawah implisit, Persamaan (14.6) dimodifikasi menjadi

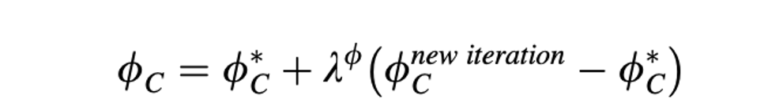
di mana βˆ…π‘* adalah nilai βˆ…π‘ dari iterasi sebelumnya. Dalam pendekatan relaksasi Patankar, βˆ…π‘(𝑛𝑒𝑀 π‘–π‘‘π‘’π‘Ÿπ‘Žπ‘‘π‘–π‘œπ‘›) iterasi baru dalam Persamaan (14.7) digantikan oleh ekspresi yang setara dari

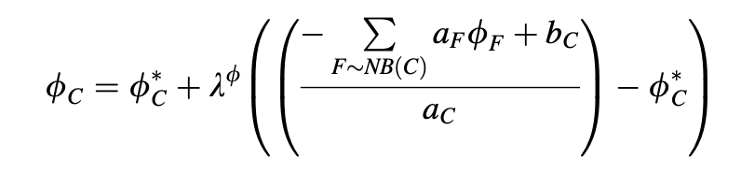
Mengatur ulang, persamaannya menjadi

Dalam Persamaan (14.9), faktor relaksasi πœ†βˆ… memodifikasi koefisien diagonal dan sisi kanan tanpa memodifikasi persamaan secara matematis. Karena πœ†βˆ…<1, relaksasi bawah meningkatkan dominasi diagonal dari sistem aljabar dan meningkatkan stabilitas solver linear iteratif. Ini adalah keuntungan penting jika dibandingkan dengan pendekatan eksplisit. Namun, perlu dicatat bahwa relaksasi implisit menerapkan hubungan yang berkorelasi dengan koefisien diagonal. Oleh karena itu, relaksasi akan lebih besar untuk koefisien diagonal yang lebih besar, yang berarti relaksasi yang lebih besar lebih penting untuk volume kontrol yang lebih kecil. Hal ini didemonstrasikan dalam bagian berikutnya.