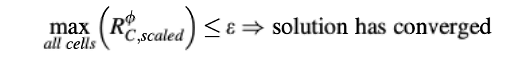Normalization of the Residual
Tingkat residu absolut adalah fungsi yang kuat dari variabel ∅. Oleh karena itu, variabel yang berbeda menghasilkan tingkat 𝑅𝐶∅ yang berbeda pula. Hal ini membuat sulit untuk memahami apakah suatu solusi telah konvergen atau tidak. Dalam kasus seperti itu, pemahaman yang lebih baik dapat diperoleh melalui penskalaan residu yang berbeda dengan membaginya dengan aliran maksimum masing-masing. Mengingat bahwa 𝑎𝐶 mewakili jumlah aliran di atas elemen, residu diubah skala relatif terhadap nilai lokal properti ∅ untuk memperoleh kesalahan relatif dengan membaginya dengan nilai maksimum 𝑎𝑐∅𝑐 di seluruh domain sehingga
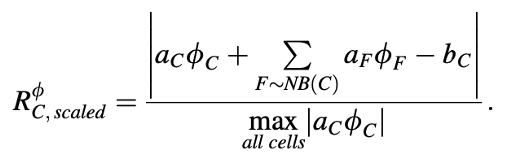
Solusi diasumsikan telah konvergen ketika nilai maksimum dari residu absolut yang telah diskalakan turun di bawah sebuah nilai yang sangat kecil e, yaitu