13.1 Introduction
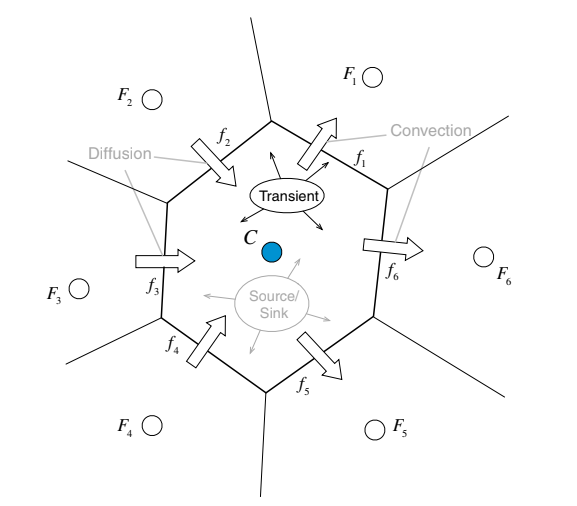
Untuk simulasi transien, persamaan-persamaan pengaturannya didiskritisasi baik dalam ruang maupun waktu. Sementara diskritisasi spasial dilakukan di domain spasial seperti yang dilakukan untuk kasus keseimbangan, diskritisasi temporal melibatkan penyusunan koordinat waktu di sepanjang mana turunan (untuk metode beda hingga) atau integral (untuk metode volume hingga) dari istilah transien dievaluasi (Gambar 13.1). Secara umum, ekspresi untuk perilaku transien, atau evolusi waktu, dari suatu variabel φ diatur oleh persamaan dalam bentuk:


Di mana fungsi adalah operator spasial yang mencakup semua istilah non-transien (konveksi, adveksi, sumber, dll.) dan
adalah operator transien, kedua-duanya ditampilkan dalam Gambar 13.1. Mengintegrasikan Persamaan (13.1) di atas suatu elemen C (Gambar 13.2) menghasilkan:
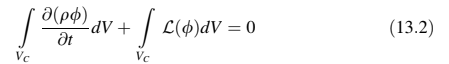
Setelah dilakukan diskritisasi spasial sekitar pusat massa volume, persamaan tersebut menjadi:
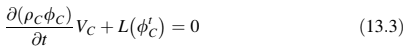
di mana adalah volume elemen diskritisasi dan
C adalah operator diskritisasi spasial yang dinyatakan pada beberapa waktu referensi t, yang dapat ditulis dalam bentuk aljabar sebagai

Dalam Persamaan (13.3), persamaan diskrit keseimbangan dikembalikan saat Hal ini juga berlaku ketika keseimbangan dikembalikan melalui pergerakan waktu, yaitu, saat
C. Hal ini menjamin bahwa solusi yang diperoleh ketika keseimbangan tercapai sama dengan yang akan diperoleh dengan masalah yang diselesaikan secara langsung sebagai masalah keseimbangan.
Untuk diskritisasi istilah transien, praktiknya secara tradisional adalah mengikuti pendekatan beda hingga [1–3], di mana ekspansi deret Taylor dari digunakan untuk mengekspresikan turunan dalam bentuk nilai nodal diskrit. Dalam bab ini, prosedur lain yang lebih sesuai dengan pendekatan volume hingga juga akan disajikan. Dalam konteks ini,
diintegrasikan selama elemen temporal [4] dan diubah menjadi fluks permukaan dengan cara yang mirip dengan yang dilakukan dengan skema konveksi, kecuali bahwa diskritisasi sekarang dilakukan sepanjang sumbu transien.
