16.5 Persamaan Koreksi Tekanan
Persamaan koreksi tekanan untuk aliran dapat dipadatkan diperoleh dengan perluasan sederhana dari persamaan untuk aliran tidak dapat dipadatkan. Perbedaannya terkait dengan variasi kepadatan yang diperhitungkan dengan mendefinisikan medan koreksi kepadatan dan menghubungkannya dengan medan koreksi tekanan melalui hubungan tekanan-kepadatan. Namun, ini menghasilkan perbedaan substansial dalam perlakuan kondisi batas, seperti akan dijelaskan nanti dalam bab ini. Untuk gas ideal, hubungan antara tekanan dan kepadatan dituliskan sebagai
Dengan menggunakan hubungan ini, sebuah persamaan yang menghubungkan koreksi kepadatan dengan koreksi tekanan dapat diperoleh dengan memperluas Persamaan (16.8) melalui deret Taylor sehingga menghasilkan
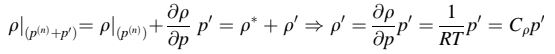
Bidang tekanan yang dikoreksi, kepadatan, kecepatan, dan laju aliran massa didefinisikan sebagai
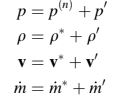
dan persamaan kontinuitas semi-terdiskritisasi dapat ditulis dalam hal medan koreksi sebagai

di mana
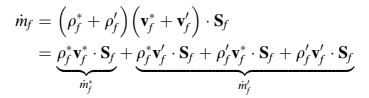
Suku koreksi orde kedua biasanya diabaikan karena jauh lebih kecil dari suku-suku lainnya. Aproksimasi ini tidak memengaruhi laju konvergensi kecuali selama beberapa iterasi pertama dari proses solusi. Selain itu, solusi akhir tidak terpengaruh, karena pada saat konvergensi, medan koreksi menghilang.
Menggunakan interpolasi Rhie-Chow untuk dan
dan
masing-masing diekspresikan sebagai

dan
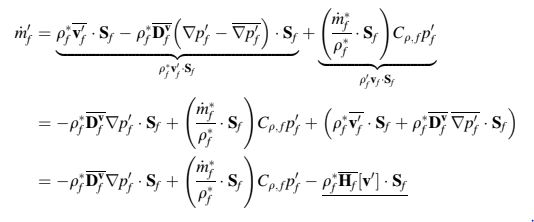
di mana suku orde kedua diabaikan. Perhatikan penggantian dengan
Suku yang digarisbawahi dalam Persamaan (16.14) menyajikan kesulitan yang sama dengan algoritma yang tidak dapat dipadatkan dan biasanya dihilangkan dari persamaan. Dengan mengabaikan suku ini, koreksi laju aliran massa menjadi
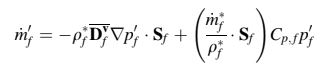
di mana suku pertama di sebelah kanan persamaan (16.15) mirip dengan yang muncul dalam aliran tidak dapat dipadatkan sementara suku kedua adalah kontribusi koreksi kepadatan baru. Suku kedua ini penting karena mengubah persamaan koreksi tekanan dari persamaan eliptik menjadi persamaan hiperbolik yang mampu menyelesaikan gelombang kejut yang mungkin muncul pada kecepatan supersonik dan hipersonik. Ini memungkinkan algoritma SIMPLE dapat dipadatkan untuk digunakan dalam memprediksi aliran fluida pada semua kecepatan tanpa memerlukan preconditioning khusus.
Lebih banyak wawasan dapat diperoleh melalui prosedur normalisasi sederhana di mana Persamaan (16.15) dibagi dengan menghasilkan faktor pembobotan 1 untuk suku
dan faktor pembobotan yang berkaitan dengan
(di mana M adalah bilangan Mach dari aliran) untuk suku
yaitu

Untuk aliran pada nilai bilangan Mach yang rendah, suku koreksi mendominasi mengembalikan persamaan ke bentuk eliptik seperti dalam kasus tidak dapat dipadatkan. Di sisi lain, untuk aliran pada nilai bilangan Mach yang sangat tinggi, suku koreksi
tidak dapat lagi diabaikan memberikan karakter hiperbolik pada persamaan koreksi. Perilaku gabungan ini memungkinkan prediksi aliran fluida pada semua kecepatan.
Substitusi Persamaan (16.14) dalam persamaan kontinuitas, Persamaan (16.11), menghasilkan bentuk dapat dipadatkan dari persamaan koreksi tekanan dan ditulis sebagai
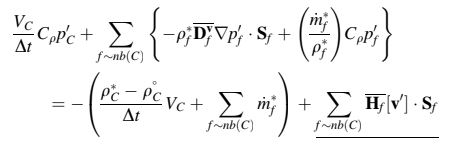
Sekali lagi, perlakuan terhadap suku yang digarisbawahi menghasilkan berbagai varian dari keluarga algoritma SIMPLE. Dengan menghilangkan suku yang digarisbawahi, persamaan koreksi tekanan untuk algoritma SIMPLE diperoleh sebagai

Persamaan (16.18) dapat diperoleh secara langsung dengan mensubstitusikan Persamaan (16.15) ke dalam Persamaan (16.11). Penting untuk menekankan bahwa suku mirip adveksi muncul secara alami selama penurunan persamaan koreksi tekanan dan kehadirannya sangat penting untuk kemampuan algoritma dalam menyelesaikan aliran pada semua kecepatan. Selain itu, untuk aliran pada nilai Mach yang tinggi, koreksi kepadatan diadveksi (yaitu, menunjukkan perilaku hiperbolik) dan operator matematika yang menggambarkan fenomena ini adalah operator divergensi orde pertama. Dengan demikian, berbeda dengan aliran tidak dapat dipadatkan di mana hanya suku mirip difusi yang hadir yang menyiratkan bahwa persamaan koreksi tekanan menunjukkan perilaku eliptik, solusi koreksi tekanan dalam bentuk tidak lagi memenuhi persamaan. Ini menunjukkan bahwa sementara untuk aliran tidak dapat dipadatkan nilai tekanan apa pun dapat ditetapkan sebagai kondisi batas tanpa memengaruhi solusi, untuk aliran dapat dipadatkan, penting untuk menentukan nilai tekanan yang tepat di batas karena nilai yang dipilih akan memengaruhi solusi akhir.
Perlu juga dicatat bahwa karena pada saat konvergensi medan koreksi adalah nol, urutan skema yang digunakan untuk mendiskritisasi suku mirip adveksi tidak memiliki konsekuensi pada akurasi hasil akhir. Namun, hal ini tidak berlaku untuk dimana penggunaan skema orde tinggi dalam evaluasinya memperbaiki sifat penangkapan kejut algoritma. Oleh karena itu, untuk meningkatkan ketahanan, berguna untuk menggunakan skema upwind untuk diskritisasi suku mirip adveksi. Selanjutnya, dengan mengabaikan kontribusi non-ortogonal dari suku mirip difusi seperti yang dijelaskan di Bab 15, persamaan koreksi tekanan dan koefisiennya menjadi

Setelah menghitung medan koreksi tekanan dengan memecahkan Persamaan (16.19), bidang kecepatan, tekanan, kepadatan, dan laju aliran massa dikoreksi menggunakan persamaan-persamaan berikut:

di mana adalah faktor relaksasi bawah untuk kepadatan.
