13.3.5 Crank-Nicholson (Central Difference Profile)
Crank-Nicholson (Central difference profile). Dengan dihitung menggunakan interpolasi linear antara simpul “Upwind” dan “Downwind”, skema Crank-Nicolson seperti yang ditunjukkan dalam Gambar 13.13 diperoleh. Untuk langkah waktu yang seragam, ini dinyatakan secara matematis sebagai
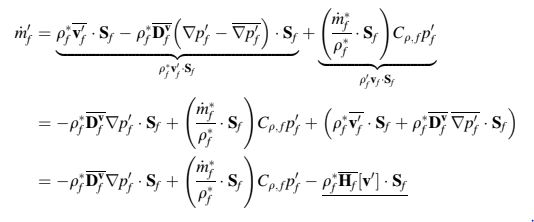
Menggantikan dalam Persamaan (13.57), persamaan terdiskritisasi menjadi

Koefisien linearisasi untuk skema CN dapat ditulis sebagai
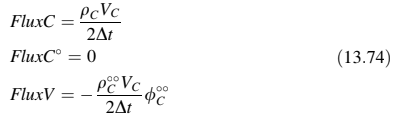

Garis-garis bantu yang ditunjukkan dalam Gambar 13.9 mengindikasikan bahwa skema ini eksplisit dengan nilai pada tingkatdihitung secara eksplisit dari nilai pada waktu t dan
Oleh karena itu, stabilitasnya dibatasi oleh batas CFL. Sekali lagi, dengan cara yang mirip dengan formulasi perbedaan hingga, ini dapat direformulasikan dalam prosedur dua langkah menggunakan Persamaan (13.48) dan (13.49), yaitu, langkah Euler implisit orde pertama diikuti oleh langkah Euler eksplisit yang dimodifikasi dalam bentuk ekstrapolasi.
13.3.5.1 Numerical Accuracy
Mengembangkan ()pada
dan
melalui ekspansi Taylor sekitar waktu t menghasilkan

Dengan mengurangkan Persamaan (13.75) dari Persamaan (13.76), persamaan berikut diperoleh:
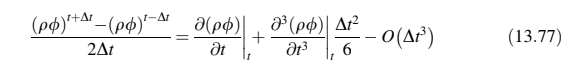
Penggantian ke dalam Persamaan (13.73) memberikan

mengkonfirmasi bahwa skema ini akurat hingga orde kedua. Turunan orde tiga adalah istilah dispersif yang menghasilkan ketidakstabilan.
