Exercises
Latihan 1
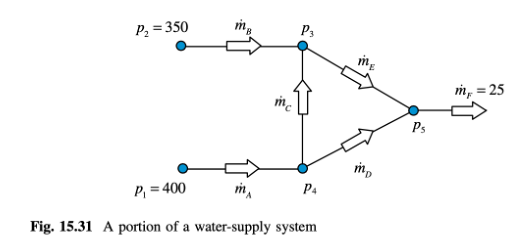
Sebuah bagian dari sistem pasokan air ditunjukkan dalam Gambar 15.31. Laju aliran m dalam sebuah bagian pipa diberikan oleh
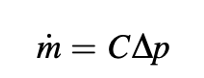
di mana Δp adalah penurunan tekanan sepanjang panjang bagian pipa, dan C adalah konduktansi hidrolik. Data berikut diketahui:

Temukan p3, p4, p5, mA; mB; mC; mD dan mE menggunakan prosedur berikut:
1. Mulailah dengan perkiraan untuk p3, p4, dan p5.
2.Hitung nilai m* berdasarkan tekanan yang ditebak.
3.Bangun persamaan koreksi tekanan dan selesaikan untuk p'3, p'4, dan p'5.
4.Perbarui tekanan dan nilai m*.
Apakah Anda perlu mengulanginya? Mengapa?
Latihan 2
Aliran satu dimensi melalui material berpori diatur oleh
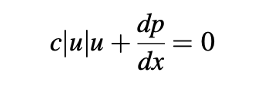
di mana c adalah sebuah konstanta. Persamaan kontinuitas adalah
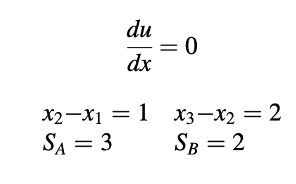
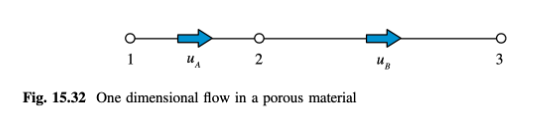
Gunakan prosedur SIMPLE untuk grid yang ditunjukkan pada Gambar 15.32 untuk menghitung p2, uA, dan uB dari data berikut:
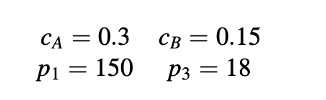
dengan ukuran dan luas di tengah setiap volume kontrol diberikan oleh
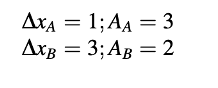
Latihan 3
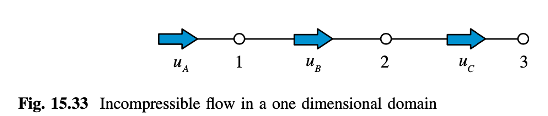
Pada situasi Steady, satu dimensi, kepadatan konstan yang ditunjukkan pada Gambar 15.33, kecepatan u dihitung di lokasi B dan C, sedangkan tekanan dihitung di lokasi 1 dan 2. Rumus koreksi kecepatan ditulis sebagai
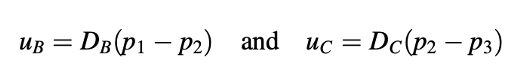
Di mana nilai DB dan DC adalah 3 dan 4, secara berturut-turut. Kondisi batasnya adalah uA = 5 dan p3 = 70.
(a) Jika pada tahap tertentu dalam proses iterasi, persamaan momentum memberikan u*B = 4 dan u*C = 6, hitung nilai-nilai p1 dan p2.
(b) Jelaskan bagaimana Anda bisa mendapatkan nilai-nilai p1 dan p3 jika kondisi batas kanan diberikan sebagai uC = 5 daripada p3 = 70.
Latihan 4
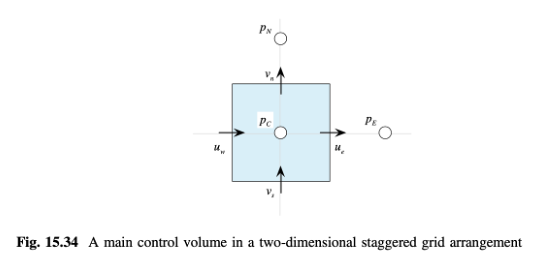
Dianggaplah volume kontrol utama seperti yang ditunjukkan dalam Gambar 15.34. Sebuah jaringan tersusun dengan komponen kecepatan u dan v disimpan seperti yang ditunjukkan. Kuantitas berikut diberikan: uw = 7, vs = 3, pN = 0, dan pE = 50. Aliran adalah steady dan densitasnya konstan. Persamaan momentum untuk ue dan vn diberikan oleh:
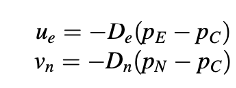
Juga diberikan De = 2, Dn = 1.6, dan volume kontrol memiliki Δx = Δy = 1.
(a) Mulai dengan nilai yang ditebak p(n) = 50, gunakan algoritma SIMPLE untuk mencari ue dan vn.
(b) Apakah perulangan iterasi diperlukan untuk masalah ini? Jelaskan.
Latihan 5
Pertimbangkan model Forchheimer satu dimensi yang disederhanakan untuk aliran dalam media berpori yang diberikan oleh
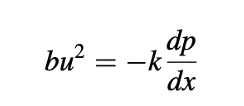
dengan persamaan kontinuitas yang diberikan oleh
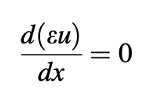
Di atas, b adalah konstanta dan ε adalah koefisien porositas yang memperhitungkan luas pori efektif. Buatlah prosedur mirip SIMPLE untuk menghitung pC, ue, dan uw untuk data berikut:
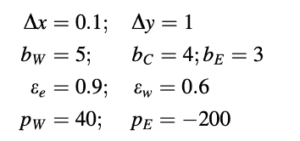
Mulailah dengan nilai awal berikut untuk kecepatan dan tekanan (Gambar 15.35):
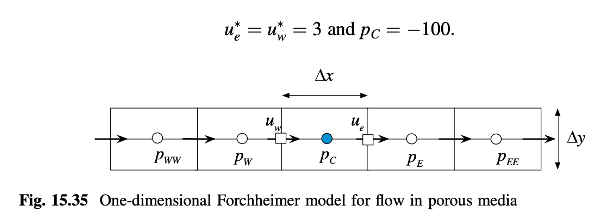
Latihan 6
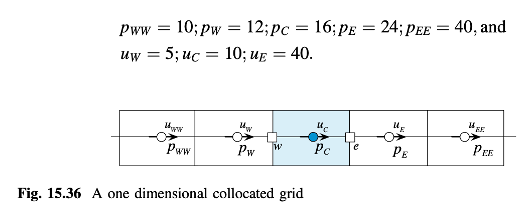
Hitung kecepatan antarmuka ue dan uw menggunakan interpolasi Rhie-Chow dan bandingkan dengan nilai rata-rata ue dan uw dengan mengetahui data berikut (Gambar 15.36):