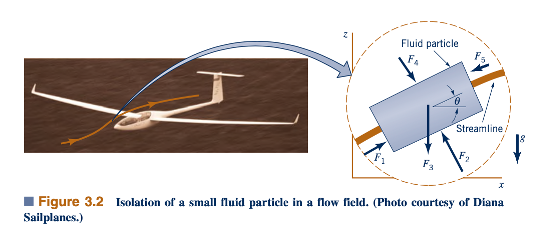
Hukum Kedua Newton
Hukum Kedua Newton. Sebagai partikel fluida bergerak dari satu lokasi ke lokasi lainnya, biasanya mengalami percepatan atau perlambatan. Menurut hukum kedua Newton tentang gerak, gaya bersih yang bekerja pada partikel fluida yang sedang dipertimbangkan harus sama dengan massa partikel tersebut dikalikan dengan percepatannya,
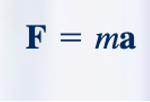
Dalam bab ini, kita mempertimbangkan gerak fluida yang tidak memiliki viskositas. Artinya, diasumsikan bahwa fluida memiliki viskositas nol. Jika viskositas nol, maka konduktivitas termal fluida juga nol dan tidak ada transfer panas yang terjadi (kecuali melalui radiasi).
Secara praktis, tidak ada fluida yang benar-benar tidak berviskositas, karena setiap fluida mendukung gaya gesekan geser ketika terkena laju perpindahan regangan. Untuk banyak situasi aliran, efek viskos dapat diabaikan relatif kecil dibandingkan dengan efek lainnya. Sebagai pendekatan pertama untuk kasus-kasus seperti itu, sering kali memungkinkan untuk mengabaikan efek viskos. Sebagai contoh, seringkali gaya-gaya viskos yang terbentuk dalam air yang mengalir mungkin beberapa derajat lebih kecil dari gaya akibat pengaruh lain, seperti gravitasi atau perbedaan tekanan. Namun, untuk situasi aliran air lainnya, efek viskos dapat menjadi yang dominan. Demikian pula, efek viskos yang terkait dengan aliran gas sering dianggap tidak signifikan, meskipun dalam beberapa keadaan mereka sangat penting.
Kita mengasumsikan bahwa gerak fluida diatur oleh gaya tekanan dan gravitasi saja dan memeriksa hukum kedua Newton sebagaimana berlaku untuk partikel fluida dalam bentuk:
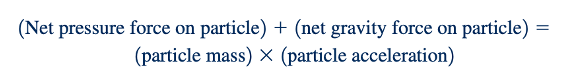
Hasil interaksi antara tekanan, gravitasi, dan percepatan memberikan banyak aplikasi yang berguna dalam mekanika fluida.
Untuk menerapkan hukum kedua Newton pada fluida (atau benda lainnya), kita harus menentukan sistem koordinat yang sesuai untuk menggambarkan gerakan tersebut. Secara umum, gerakan akan tiga dimensi dan tidak stabil sehingga diperlukan tiga koordinat ruang dan waktu untuk menggambarkannya. Ada banyak sistem koordinat yang tersedia, termasuk yang paling sering digunakan adalah sistem koordinat kartesian (x, y, z) dan sistem koordinat silinder (r, θ, z) seperti yang ditunjukkan oleh gambar di samping. Biasanya geometri aliran tertentu menentukan sistem mana yang paling sesuai.
Dalam bab ini, kami akan mempertimbangkan gerakan dua dimensi seperti yang terbatas pada bidang x–z seperti yang ditunjukkan pada Gambar 3.1a. Jelas bahwa kita bisa memilih untuk menggambarkan aliran dalam hal komponen akselerasi dan gaya dalam arah koordinat x dan z. Persamaan yang dihasilkan sering disebut sebagai bentuk dua dimensi dari persamaan gerak Euler dalam koordinat kartesian berbentuk persegi. Pendekatan ini akan dibahas dalam Bab 6.
Seperti yang dilakukan dalam studi dinamika, gerakan setiap partikel fluida dijelaskan dalam istilah vektor kecepatannya, V, yang didefinisikan sebagai perubahan waktu dari posisi partikel. Kecepatan partikel adalah besaran vektor dengan magnitudo (kecepatan, V = |V|) dan arah. Saat partikel bergerak, ia mengikuti jalur tertentu, yang bentuknya ditentukan oleh kecepatan partikel. Lokasi partikel sepanjang jalur merupakan fungsi dari di mana partikel tersebut mulai pada waktu awal dan kecepatannya sepanjang jalur. Jika aliran tersebut adalah aliran stabil (tidak ada yang berubah dengan waktu di lokasi tertentu dalam medan aliran), setiap partikel berikutnya yang melewati suatu titik tertentu [seperti titik (1) pada Gambar 3.1a] akan mengikuti jalur yang sama. Untuk kasus tersebut, jalur tersebut adalah garis tetap dalam bidang x–z. Partikel tetangga yang melewati di kedua sisi titik (1) mengikuti jalur mereka sendiri, yang mungkin memiliki bentuk yang berbeda dengan yang melewati titik (1). Seluruh bidang x–z diisi dengan jalur-jalur seperti itu.
garis-garis yang berupa tangen terhadap vektor kecepatannya sepanjang medan aliran disebut garis aliran. Untuk banyak situasi, lebih mudah untuk menjelaskan aliran dalam hal ini.
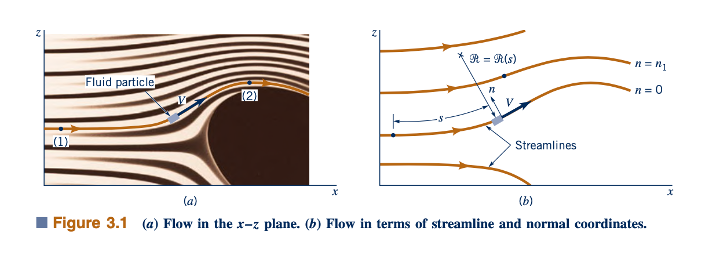
Koordinat "garis aliran" didasarkan pada garis aliran seperti yang diilustrasikan dalam Gambar 3.1b. Gerakan partikel dijelaskan dalam hal jaraknya, s = s(t), sepanjang garis aliran dari suatu asal yang nyaman dan jari-jari lengkung lokal garis aliran, r = r(s). Jarak sepanjang garis aliran berkaitan dengan kecepatan partikel dengan V = ds/dt, dan jari-jari lengkung berkaitan dengan bentuk garis aliran. Selain dari koordinat sepanjang garis aliran, s, koordinat normal terhadap garis aliran, n, seperti yang ditunjukkan dalam Gambar 3.1b, juga akan berguna.
Untuk menerapkan hukum kedua Newton pada partikel yang mengalir sepanjang garis alirannya, kita harus menulis percepatan partikel dalam hal koordinat garis aliran. Menurut definisi, percepatan adalah laju perubahan waktu kecepatan partikel, a = dV/dt. Untuk aliran dua dimensi dalam bidang x–z, percepatan memiliki dua komponen—satu sepanjang garis aliran, as, percepatan sepanjang aliran, dan satu normal terhadap garis aliran, an, percepatan normal.
Percepatan sepanjang aliran timbul dari fakta bahwa kecepatan partikel umumnya bervariasi sepanjang garis aliran, V = V(s). Sebagai contoh, dalam Gambar 3.1a kecepatan mungkin 50 ft/s di titik (1) dan 100 ft/s di titik (2). Oleh karena itu, dengan menggunakan aturan rantai diferensiasi, komponen s dari percepatan diberikan oleh as = dV/dt = 10(V₀(s))²(ds/dt) = 10(V₀(s)V). Kami telah menggunakan fakta bahwa kecepatan adalah laju perubahan waktu jarak, V = ds/dt. Perhatikan bahwa percepatan sepanjang aliran adalah hasil kali laju perubahan kecepatan dengan jarak sepanjang garis aliran, V₀(s), dan kecepatan, V. Karena V₀(s) bisa positif, negatif, atau nol, maka percepatan sepanjang aliran dapat menjadi positif (percepatan), negatif (perlambatan), atau nol (kecepatan konstan).
Komponen normal dari percepatan, percepatan sentrifugal, diberikan dalam hal kecepatan partikel dan radius lengkung jalurnya. Dengan demikian, a= V2/r, di mana baik V maupun r dapat bervariasi sepanjang garis aliran. Persamaan untuk percepatan ini seharusnya sudah familiar dari studi gerak partikel dalam fisika atau dinamika. Sebuah turunan lebih lengkap dan diskusi tentang topik-topik ini dapat ditemukan di Bab 4.
Jadi, komponen percepatan pada arah s dan n, as dan an, diberikan oleh
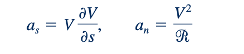
Di mana r adalah jari-jari lokal dari lengkungan streamline, dan s adalah jarak yang diukur sepanjang streamline dari suatu titik awal arbitrer. Secara umum, ada percepatan sepanjang streamline (karena kecepatan partikel berubah sepanjang jalurnya, ds/dV≠0) dan percepatan normal terhadap streamline (karena partikel tidak mengalir lurus, R ≠ ∞). Berbagai aliran dan percepatan yang terkait dengan mereka ditunjukkan dalam gambar di pinggir teks. Seperti yang dibahas dalam Bagian 3.6.2, untuk aliran inkompressibel, kecepatan berbanding terbalik dengan jarak antara streamlines. Oleh karena itu, streamlines yang berkonvergensi menghasilkan percepatan sepanjang streamline yang positif. Untuk menghasilkan percepatan ini, harus ada gaya bersih yang tidak nol pada partikel fluida.